Lenses – JEE First

Lensing by oil on water

May 23rd, 2022jeefirst0 Comments

JEE Advanced 2011 Paper 2, Question 36

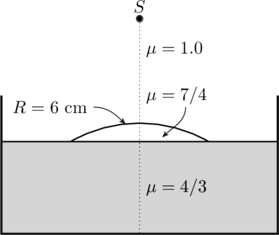
Water (with refractive index $=\frac{4}{3}$ ) in a tank is $18 \mathrm{~cm}$ deep. Oil of refractive index $\frac{7}{4}$ lies on water making a convex surface of radius of curvature $R=6 {\rm ~cm}$ as shown. Consider oil to act as a thin lens. An object ‘ $S$ ’ is placed $24 \mathrm{~cm}$ above water surface. The location of its image is at ‘ $x$ ’ cm above the bottom of the tank. What is ‘ $x$ ’?

Rendered by QuickLaTeX.com

Solution

To find the location of the final image we consider the oil and the water in the tank as a combination of two elements: a lens and a …

Lenses II: Image formation

May 15th, 2022jeefirst0 Comments

Continuing our discussion from the previous chapter, we can use the thin lens equation and our knowledge of the signs of $f$ , to determine the position, orientation, and magnification of the image for different object distances $p$ . This is similar to the analysis we did for mirrors here. The results are summarized in the table below.

Converging lens

The focal length of a converging lens is positive. That means light from infinity will be brought to focus behind the lens. We will begin our analysis there.

Starting from $p = \infty$

Consider an object kept in front of a converging lens. …

Lenses I: The thin lens equation

May 14th, 2022jeefirst0 Comments

A lens is a refracting element with two curved surfaces. Light changes direction as it refracts through each of these surfaces. If the thickness of the lens is small compared to the radius of curvature of each surface, we can think of light as bending just once at the central plane of the lens. This approximation is justified more rigorously in chapter 27 of the Feynman lectures. For our present discussion we start with equation (27.12) from that book, called the thin lens equation,

(1) $\begin{equation*} \frac{1}{p} + \frac{1}{q} = \frac{1}{f} , \end{equation*}$

where $p$ is the object distance from the lens, $q$ is the image distance, and …

Three glass cylinders

January 24th, 2022jeefirst0 Comments

JEE Advanced 2019 Paper 2, Question 6

Three glass cylinders of equal height $H=30 \, {\rm cm}$ and same refractive index $n=1.5$ are placed on a horizontal surface as shown in figure. Cylinder I has a flat top, cylinder II has a convex top and cylinder III has a concave top. The radii of curvature of the two curved tops are same ( $R=3 \, {\rm m}$ ). If $H_{1}, H_{2}$ , and $H_{3}$ are the apparent depths of a point $X$ on the bottom of the three cylinders, respectively, the correct statement(s) is/are:

Rendered by QuickLaTeX.com

$H_{2}>H_{1}$
$H_{3}>H_{1}$
$H_{2}>H_{3}$
$0.8 \, {\rm cm} < (H_{2}-H_{1}) < 0.9 \, {\rm cm}$

Solution

We can get some intuition for what happens in each case by drawing some simple ray diagrams, as …

Convex lens with two materials

January 2nd, 2022jeefirst0 Comments

JEE Advanced 2019 Paper 1, Question 10

A thin convex lens is made of two materials with refractive indices $n_1$ and $n_2$ as shown in figure. The radius of curvature of the left and right spherical surfaces are equal. $f$ is the focal length of the lens when $n_1 = n_2 = n$ . The focal length is $f + \Delta f$ when $n_1 = n$ and $n_2 = n + \Delta n$ . Assuming $\Delta n \ll (n-1)$ and $1 < n < 2$ , the correct statement(s) is/are,

Rendered by QuickLaTeX.com

$\bigg| \frac{\Delta f}{f} \bigg| < \bigg| \frac{\Delta n}{n} \bigg|$
For $n=1.5, \Delta n = 10^{-3}$ and $f = 20$ cm, the value of $|\Delta f|$ will be 0.02 cm (round off to $2^{\rm nd}$ decimal place).
If $\frac{\Delta n}{n} < 0$ then $\frac{\Delta f}{f} > 0$
The relation between $\frac{\Delta f}{f}$ and $\frac{\Delta n}{n}$ remains unchanged if both the convex surfaces are replaced by concave surfaces of the same radius of curvature.

Related …