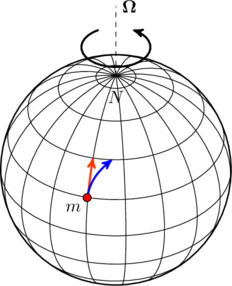
Imagine a mass ![]() moving on the surface of a rotating sphere. For instance, the mass could be parcel of air moving away from a high pressure region in the Earth’s atmosphere. It experiences a Coriolis force which, in the example shown in the figure below, pushes it from its original trajectory (orange) to move eastward (blue). Why does this happen, and how do we understand it intuitively?
moving on the surface of a rotating sphere. For instance, the mass could be parcel of air moving away from a high pressure region in the Earth’s atmosphere. It experiences a Coriolis force which, in the example shown in the figure below, pushes it from its original trajectory (orange) to move eastward (blue). Why does this happen, and how do we understand it intuitively?
Formally, the Coriolis force on ![]() is given by
is given by
(1) ![]()
where ![]() is the angular velocity of the rotating frame (Earth), and
is the angular velocity of the rotating frame (Earth), and ![]() is the velocity of
is the velocity of ![]() as seen by an observer on the Earth’s …
as seen by an observer on the Earth’s …