JEE Advanced 2013 Paper 1, Question 12
A solid sphere of radius ![]() and density
and density ![]() is attached to one end of a mass-less spring of force constant
is attached to one end of a mass-less spring of force constant ![]() . The other end of the spring is connected to another solid sphere of radius
. The other end of the spring is connected to another solid sphere of radius ![]() and density
and density ![]() . The complete arrangement is placed in a liquid of density
. The complete arrangement is placed in a liquid of density ![]() and is allowed to reach equilibrium. The correct statement(s) is (are)
and is allowed to reach equilibrium. The correct statement(s) is (are)
- the net elongation of the spring is
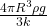 .
. - the net elongation of the spring is
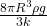
- the light sphere is partially submerged.
- the light sphere is completely submerged.
Solution
Recall that the buoyant force experienced by an object is equal to the weight of the liquid displaced by the object. This is Archimedes’ principle. Let us first consider what happens if the two spheres were placed in the liquid without a spring connecting them. The lighter sphere would float since it is not as dense as the liquid. The heavier sphere, with density ![]() would experience a net downward force of
would experience a net downward force of ![]() . Here
. Here ![]() is the buoyant force due the liquid displaced, and
is the buoyant force due the liquid displaced, and ![]() is the volume of the sphere.
is the volume of the sphere.
If the two spheres are connected by a spring, the downward force ![]() of the heavier sphere is transmitted to the lighter one as tension
of the heavier sphere is transmitted to the lighter one as tension ![]() , and it pulls it down. In fact, the lighter sphere will be completely submerged under its own weight plus
, and it pulls it down. In fact, the lighter sphere will be completely submerged under its own weight plus ![]() since
since ![]() is also the maximum buoyant force the liquid can exert on the sphere. Free body diagrams indicating the forces are show below.
is also the maximum buoyant force the liquid can exert on the sphere. Free body diagrams indicating the forces are show below.
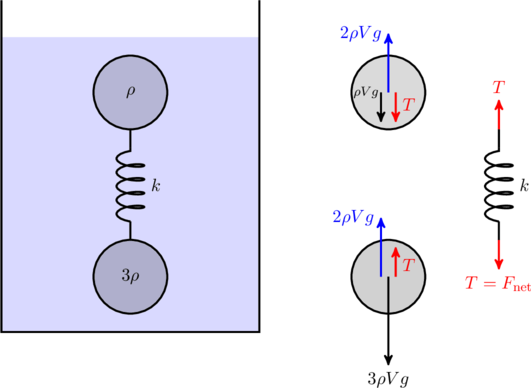
For the problem at hand, we need to find the elongation of the spring. This is simply
(1) ![]()
Note: If you’re wondering why ![]() rather than
rather than ![]() , recall that if we fix one end of a spring to a rigid wall and pull on the other end with a force
, recall that if we fix one end of a spring to a rigid wall and pull on the other end with a force ![]() the spring extends by
the spring extends by ![]() . The free body diagram of the spring will show
. The free body diagram of the spring will show ![]() acting at both ends of the string, just like the present case.
acting at both ends of the string, just like the present case.
Thus, options (A) and (D) are correct.
Bonus problem
In the above problem we implicitly assumed that there was enough water in the container for the sphere-spring arrangement to be completely submerged. What if that were not the case? That is, imagine placing the spheres with the spring into an empty container, and then filling it up with the liquid to a height ![]() such that a fraction
such that a fraction ![]() of the lighter sphere is sticking out above the water surface. Find the elongation of the spring in this situation.
of the lighter sphere is sticking out above the water surface. Find the elongation of the spring in this situation.
Solution
If the lighter sphere is only partially submerged, the buoyant force on it (![]() ) is not sufficient to balance the net downward force on the heavier sphere. Therefore the heavier sphere will touch the bottom of the container, as shown in the figure below.
) is not sufficient to balance the net downward force on the heavier sphere. Therefore the heavier sphere will touch the bottom of the container, as shown in the figure below.
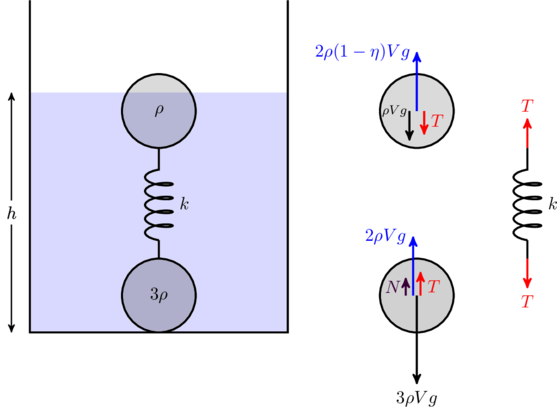
The floor of the container will exert a normal force ![]() on the heavier sphere, which makes up for the loss in buoyancy from the lighter sphere. Therefore
on the heavier sphere, which makes up for the loss in buoyancy from the lighter sphere. Therefore ![]() . We can also arrive at this by writing down the force balance equation on each sphere,
. We can also arrive at this by writing down the force balance equation on each sphere,
(2) ![]()
The first equation also gives us the tension, ![]() , which stretches the spring by
, which stretches the spring by
(3) ![]()
If the lighter sphere were completely submerged ![]() would be zero and we recover (1). If
would be zero and we recover (1). If ![]() , there is no tension in the spring. That is, with half the lighter sphere above the water surface the buoyant force on it (
, there is no tension in the spring. That is, with half the lighter sphere above the water surface the buoyant force on it (![]() ) is barely sufficient to balance out its own weight; there is no force left to pull up the heavier sphere.
) is barely sufficient to balance out its own weight; there is no force left to pull up the heavier sphere.
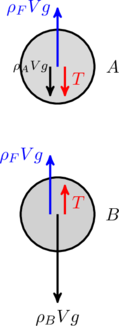
JEE Advanced 2011 Paper 2, Question 29
Two solid spheres ![]() and
and ![]() of equal volumes but of different densities
of equal volumes but of different densities ![]() and
and ![]() are connected by a string. They are fully immersed in a fluid of density
are connected by a string. They are fully immersed in a fluid of density ![]() . They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if
. They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if
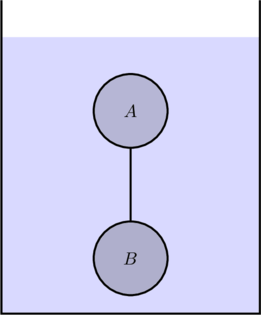
Solution
This problem is essentially the same as the one above, with the only difference being that the net downward force from the heavier sphere transmitted to the lighter sphere via an inextensible string. At equilibrium the forces on each sphere must add up to zero (see figure below),
(4) ![]()
For the lighter sphere to hold up the heavier one we must have ![]() . This is apparent from the above equations when we note that
. This is apparent from the above equations when we note that ![]() . So options (A), (B) and (D) are correct.
. So options (A), (B) and (D) are correct.