Problem 3.231 from Irodov.
A current ![]() flows along a lengthy straight wire, as shown in the figure below. From the point O the current spreads radially all over an infinite conducting plane perpendicular to the wire. Find the magnetic field above and below the plane.
flows along a lengthy straight wire, as shown in the figure below. From the point O the current spreads radially all over an infinite conducting plane perpendicular to the wire. Find the magnetic field above and below the plane.
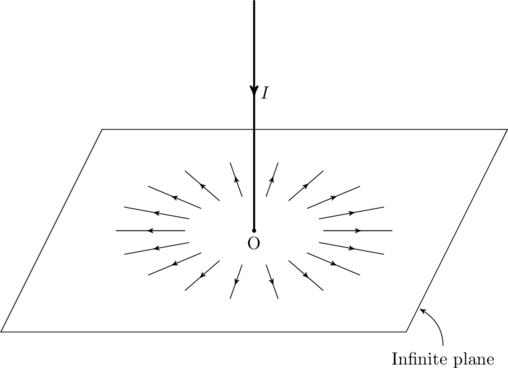
Solution:
We will use this problem to demonstrate the use of Ampere’s law, starting with some simple scenarios. Our goal is to understand how to exploit symmetries in the problem to compute the magnetic field from a given current distribution. We begin by stating the law.
(1) ![]()
The integral on the left hand side is carried out over an imaginary loop in space, broken down into line elements ![]() . In general, it is difficult to calculate this integral explicitly. However, if the problem exhibits certain symmetries and we are clever with our choice of the imaginary loop, the calculation simplifies a great deal.
. In general, it is difficult to calculate this integral explicitly. However, if the problem exhibits certain symmetries and we are clever with our choice of the imaginary loop, the calculation simplifies a great deal.
As an illustration, consider an infinitely long wire carrying a current ![]() . By rotational symmetry, the magnetic field at all points a distance
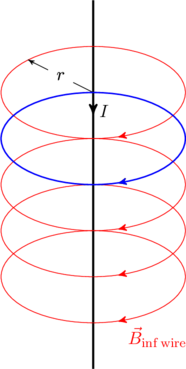
. By rotational symmetry, the magnetic field at all points a distance ![]() from an infinite wire must have the same magnitude. What about the direction of the field? A field emanating radially outward from the wire, or a field parallel to the wire everywhere would both be invariant under a rotation about the wire. However, magnetic field lines cannot begin or end (there are no magnetic monopoles), so a radial field is out of the question. We also know from Biot-Savart law that the magnetic field must be perpendicular to the current, so a parallel field is also incorrect. The only remaining possibility is that the magnetic field due to the wire forms closed circular loops around the wire, as shown in the figure. The direction of the field can be determined by the right hand grip rule. We also realize that placing the Amperian loop along one of these field lines would make the integral in (1) straightforward,
from an infinite wire must have the same magnitude. What about the direction of the field? A field emanating radially outward from the wire, or a field parallel to the wire everywhere would both be invariant under a rotation about the wire. However, magnetic field lines cannot begin or end (there are no magnetic monopoles), so a radial field is out of the question. We also know from Biot-Savart law that the magnetic field must be perpendicular to the current, so a parallel field is also incorrect. The only remaining possibility is that the magnetic field due to the wire forms closed circular loops around the wire, as shown in the figure. The direction of the field can be determined by the right hand grip rule. We also realize that placing the Amperian loop along one of these field lines would make the integral in (1) straightforward,
(2) ![]()
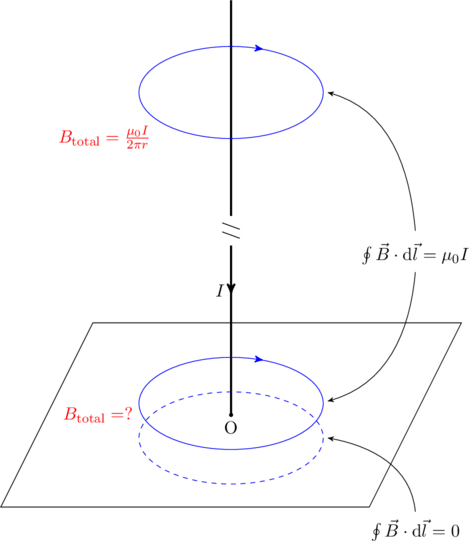
In arriving at this result we have also used used the translational symmetry of the problem implicitly. That is, we could have used an Amperian loop centered at any point along the wire and obtained the same ![]() . This is not true for the original problem we want to solve — from the figure above we would expect that, at a distance
. This is not true for the original problem we want to solve — from the figure above we would expect that, at a distance ![]() from the wire, the magnetic field near the plane does not have to be the same as the field far from the plane (see figure below). In the latter case, the magnetic field would resemble that due to an infinite wire, since the influence of the radial current on the plane must wane as we move farther away from it. Therefore, to good accuracy
from the wire, the magnetic field near the plane does not have to be the same as the field far from the plane (see figure below). In the latter case, the magnetic field would resemble that due to an infinite wire, since the influence of the radial current on the plane must wane as we move farther away from it. Therefore, to good accuracy
(3) ![]()
The problem still has rotational symmetry eveywhere, since the current distribution remains unchanged if we rotate the setup about the point ![]() with the straight wire as the axis of rotation. Therefore, the magnetic field generated by the currents must also be invariant under such a rotation. Could we consider a circular Amperian loop
with the straight wire as the axis of rotation. Therefore, the magnetic field generated by the currents must also be invariant under such a rotation. Could we consider a circular Amperian loop ![]() around the wire, close to
around the wire, close to ![]() , and conclude that the magnetic field there is also
, and conclude that the magnetic field there is also ![]() ? Does an Amperian loop
? Does an Amperian loop ![]() below the plane tell us that the field there is zero? No, because we cannot be sure that the field is still in the form of closed circular loops in the region immediately above or below the plane. Let us therefore analyze the field in this region carefully.
below the plane tell us that the field there is zero? No, because we cannot be sure that the field is still in the form of closed circular loops in the region immediately above or below the plane. Let us therefore analyze the field in this region carefully.
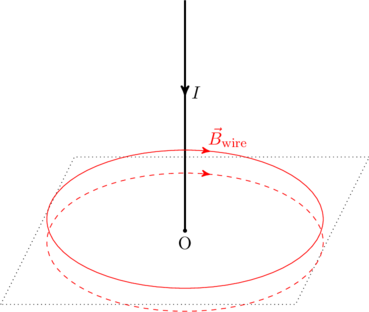
To determine ![]() near the plane we compute the magnetic fields from the straight wire and the plane separately, and add them together at the end (this is superposition). First, we consider the semi-infinite wire carrying the current to
near the plane we compute the magnetic fields from the straight wire and the plane separately, and add them together at the end (this is superposition). First, we consider the semi-infinite wire carrying the current to ![]() . The field generated by this wire immediately above and below the plane can be computed using Ampere’s Law by thinking of the semi-infinite wire as half of an infinite wire (again, by superposition). The magnetic field generated by the latter was found in (2).
. The field generated by this wire immediately above and below the plane can be computed using Ampere’s Law by thinking of the semi-infinite wire as half of an infinite wire (again, by superposition). The magnetic field generated by the latter was found in (2).
The field generated by the semi-infinite wire is half that, giving us
(4) ![]()
at a distance ![]() from
from ![]() , in a counterclockwise direction both above and below the plane (see figure). We can also arrive at the same result by using Biot-Savart law and integrating, as discussed in detail here. This would lead to
, in a counterclockwise direction both above and below the plane (see figure). We can also arrive at the same result by using Biot-Savart law and integrating, as discussed in detail here. This would lead to
(5) ![]()
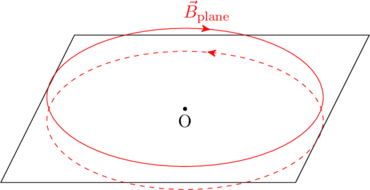
Next, we turn our attention to the radial current in the plane. A point near the plane will observe a field that is parallel to the plane. To see this explicitly, we can imagine splitting the radial current into many straight line currents, each of which produces a circular magnetic field around it. The superposition of fields from several nearby line currents creates a net magnetic field that is tangential to the plane. It also means that the field above the plane will have the opposite direction to the field below the plane. Noting that the field must also be rotationally invariant, we conclude that the magnetic field due to the plane must be in the form of closed circular loops as shown in the figure. It is directed clockwise above the plane, and anticlockwise below the plane.
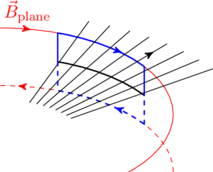
The magnitude of ![]() can be determined by applying (1) on the Amperian loop shown in blue in figure. The curved segments of this loop have been chosen to lie along lines of constant magnetic field, at a radial distance
can be determined by applying (1) on the Amperian loop shown in blue in figure. The curved segments of this loop have been chosen to lie along lines of constant magnetic field, at a radial distance ![]() from
from ![]() . The straight vertical segments are very small since we are close to the plane, therefore their contribution to line integral in (1) is negligible. The current enclosed by the Amperian loop is
. The straight vertical segments are very small since we are close to the plane, therefore their contribution to line integral in (1) is negligible. The current enclosed by the Amperian loop is ![]() , where
, where ![]() is the length of the curved segment. Therefore,
is the length of the curved segment. Therefore,
(6) ![]()
Now that we have computed the magnetic field from both the plane and the straight wire separately near the plane, we can add them together to obtain
(7) ![Rendered by QuickLaTeX.com \begin{equation*} B_{\rm total} = B_{\rm wire} + B_{\rm plane} = \begin{cases} \begin{aligned} \frac{\mu_0 I}{2 \pi r}, &\quad \text{above the plane and near it} \\[0.5em] 0, &\quad \text{below the plane} . \end{aligned} \end{cases} \end{equation*}](https://www.jeefirst.com/wp-content/ql-cache/quicklatex.com-e2a59e6a8d76ead3d3e07ff39ada82ea_l3.png)
But we know from (3) that the magnetic field above the plane and far away from it is also ![]() . This must be the field everywhere above the plane; if it weren’t there would be a component of the field that started far away from the plane and ended right above the plane, which is not allowed. Therefore, we conclude that
. This must be the field everywhere above the plane; if it weren’t there would be a component of the field that started far away from the plane and ended right above the plane, which is not allowed. Therefore, we conclude that
(8) ![Rendered by QuickLaTeX.com \begin{equation*} \boxed{ B_{\rm total} = \begin{cases} \begin{aligned} \frac{\mu_0 I}{2 \pi r}, &\quad \text{\textit{everywhere} above the plane} \\[0.5em] 0, &\quad \text{\textit{everywhere} below the plane} . \end{aligned} \end{cases} } \end{equation*}](https://www.jeefirst.com/wp-content/ql-cache/quicklatex.com-63d31a0bb5ff6334e4084875201c0fab_l3.png)
Bonus problem:
A spherical, radial current distribution emanates from a point in space. What is the magnetic field generated by this current?