Conductors – JEE First

Physics concepts and problems for the JEE

Missing energy in a rope and a capacitor

February 14th, 2022jeefirst0 Comments

Consider a uniform rope of mass density $\lambda$ coiled on a smooth horizontal table. One end is pulled straight up with a constant speed $v_0$ as shown.

Find the force exerted on the end of the rope as function of the height $y$ .
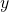Compare the power delivered to the rope with the rate of change of the rope’s mechanical energy.

(This is a problem from chapter 5 of Kleppner and Kolenkow)

Rendered by QuickLaTeX.com

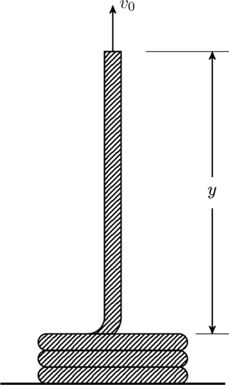
To find the force exerted at the top end, note that if we were to pull up a fixed mass with constant velocity $v_0$ , the total force on the mass should …

A spherical capacitor

January 20th, 2022jeefirst0 Comments

A spherical conducting shell with radius $b$ is concentric with a conducting ball with radius $a$ , with $a<b$ .

Compute the capacitance $C = Q / \Delta \phi$ when the shell is grounded and the ball has charge $Q$ .
Compute the capacitance when the ball is grounded and the shell has charge $Q$ .
Compute the full matrix of coefficients of capacitance for the two conductors.
Considering these conductors as a capacitor, determine its capacitance. That is, assign equal and opposite charges $\pm Q$ to the shell and the ball, and compute $C = Q / \Delta \phi$ .

Related Problem: Insulating spherical shell with a hole

Solution

(a) First, we ground the shell and give the …