Taylor Expansion – JEE First

Physics concepts and problems for the JEE

Progressive refraction through glass layers

March 4th, 2022jeefirst0 Comments

JEE Advanced 2017 Paper 1, Question 10

A monochromatic light is traveling in a medium of refractive index $n=1.6$ . It enters a stack of glass layers from the bottom side at an angle $\theta=30^{\circ}$ . The interfaces of the glass layers are parallel to each other. The refractive indices of different glass layers are monotonically decreasing as $n_{m}=n-m \Delta n$ , where $n_{m}$ is the refractive index of the $m^{\rm th}$ slab and $\Delta n=0.1$ (see the figure). The ray is refracted out parallel to the interface between the $(m-1)^{\rm th}$ and $m^{\rm th}$ slabs from the right side of the stack. What is the value of $m$ ?

Rendered by QuickLaTeX.com

Solution

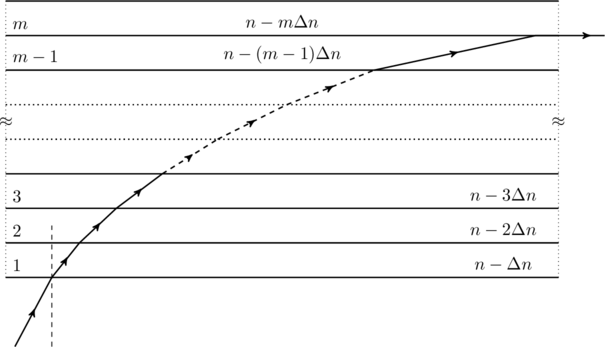
Consider the trajectory of …

Convex lens with two materials

January 2nd, 2022jeefirst0 Comments

JEE Advanced 2019 Paper 1, Question 10

A thin convex lens is made of two materials with refractive indices $n_1$ and $n_2$ as shown in figure. The radius of curvature of the left and right spherical surfaces are equal. $f$ is the focal length of the lens when $n_1 = n_2 = n$ . The focal length is $f + \Delta f$ when $n_1 = n$ and $n_2 = n + \Delta n$ . Assuming $\Delta n \ll (n-1)$ and $1 < n < 2$ , the correct statement(s) is/are,

Rendered by QuickLaTeX.com

$\bigg| \frac{\Delta f}{f} \bigg| < \bigg| \frac{\Delta n}{n} \bigg|$
For $n=1.5, \Delta n = 10^{-3}$ and $f = 20$ cm, the value of $|\Delta f|$ will be 0.02 cm (round off to $2^{\rm nd}$ decimal place).
If $\frac{\Delta n}{n} < 0$ then $\frac{\Delta f}{f} > 0$
The relation between $\frac{\Delta f}{f}$ and $\frac{\Delta n}{n}$ remains unchanged if both the convex surfaces are replaced by concave surfaces of the same radius of curvature.

Related …