Progressive refraction through glass layers

JEE Advanced 2017 Paper 1, Question 10

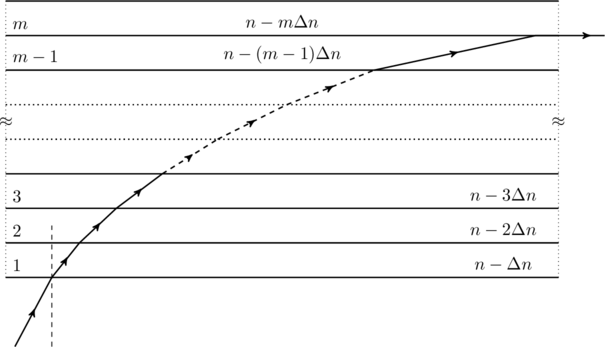
A monochromatic light is traveling in a medium of refractive index $n=1.6$ . It enters a stack of glass layers from the bottom side at an angle $\theta=30^{\circ}$ . The interfaces of the glass layers are parallel to each other. The refractive indices of different glass layers are monotonically decreasing as $n_{m}=n-m \Delta n$ , where $n_{m}$ is the refractive index of the $m^{\rm th}$ slab and $\Delta n=0.1$ (see the figure). The ray is refracted out parallel to the interface between the $(m-1)^{\rm th}$ and $m^{\rm th}$ slabs from the right side of the stack. What is the value of $m$ ?

Solution

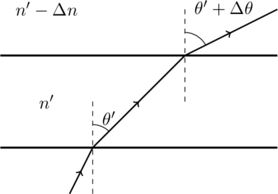
Consider the trajectory of light as it passes between two successive layers of glass with indices of refraction $n'$ and $n'-\Delta n'$ (see figure). Since light is going from an optically denser medium to a rarer one, it bends away from the normal. By Snell’s law

(1) $\begin{equation*} n' \sin \theta' = (n' + \Delta n) \sin (\theta' + \Delta \theta) . \end{equation*}$

The change $\Delta n$ is small compared to $n'$ , which means the change in the angle of refraction, $\Delta \theta$ , must also be small. Recall, the Taylor expansion of a function $f(x)$ about $x_0$ is

(2) $\begin{equation*} f(x_0 + \Delta x) = f(x_0) + \frac{{\rm d} f}{{\rm d} x}\bigg\rvert_{x_0} \Delta x + \dots . \end{equation*}$

We can use this to write $\sin (\theta' + \Delta \theta) \approx \sin \theta' + \Delta \theta \cos \theta' + \dots$ , since $\Delta \theta$ is small. Then, (1) becomes

(3) $\begin{equation*} n' \sin \theta' = (n' - \Delta n) (\sin \theta' + \Delta \theta \cos \theta' + \dots) . \end{equation*}$

Throwing away the higher order terms in $\Delta n$ and/or $\Delta \theta$ , we can reorganize this into

(4) $\begin{equation*} \Delta n \sin \theta' = n' \Delta \theta \cos \theta' \implies \frac{\Delta \theta}{\Delta n} = \frac{\tan \theta'}{n'} . \end{equation*}$

In the limit of $\Delta n \to 0$ the ratio $\frac{\Delta \theta}{\Delta n}$ becomes the derivative $\frac{{\rm d} \theta'}{{\rm d} n'}$ , and we get

(5) $\begin{equation*} \frac{{\rm d} \theta'}{{\rm d} n'} = \frac{\tan \theta'}{n'} . \end{equation*}$

We can integrate this equation,

(6) $\begin{equation*} \int_{\theta}^{\pi/2} {\rm d} \theta' \frac{\cos \theta'}{\sin \theta'} = \int_{n}^{n-m \Delta n} \frac{{\rm d} n'}{n'} , \end{equation*}$

where, the limit of integration follow from the fact that the ray starts out at an angle $\theta' = \theta$ from a glass layer of refractive index $n$ and ends up at $\theta' = \pi/2$ when $n'= n-m \Delta n$ (see figure). Carrying out the integral we obtain

(7) $\begin{equation*} \frac{1}{\sin \theta} = \frac{n-m \Delta n}{n} . \end{equation*}$

Plugging in $\sin \theta = \sin 30^\circ = 1/2$ , $n=1.6$ and $\Delta n = 0.1$ we find

(8) $\begin{equation*} \boxed{m = 8.} \end{equation*}$

Discussion: This problem demonstrates how light bends by progressive refraction through layers of decreasing refractive index. If light were incident at the bottom layer with an angle larger than $\theta$ light would get total internally reflected at or before the $m^{\rm th}$ layer. This is the same mechanism by which radio waves are reflected from the earth’s atmosphere. In particular, the refractive index of the ionosphere becomes smaller as we climb in altitude, and we can use it as a mirror to bounce off radio signals beyond the horizon just like we see in this problem.

Leave a Reply Cancel reply