A current ![]() flows along a thin wire, shaped as a regular polygon with
flows along a thin wire, shaped as a regular polygon with ![]() sides, which can be inscribed intro a circle of radius
sides, which can be inscribed intro a circle of radius ![]() . Find the magnetic field at the center of the polygon. What happens if
. Find the magnetic field at the center of the polygon. What happens if ![]() is made very large?
is made very large?
Solution:
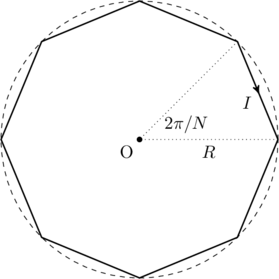
The polygon described in the problem is illustrated in the figure below, for ![]() . The magnetic field created by this structure is the superposition of fields from
. The magnetic field created by this structure is the superposition of fields from ![]() straight current carrying wires of length
straight current carrying wires of length ![]() . Therefore, we will need to find the magnetic field due to a wire of finite length first.
. Therefore, we will need to find the magnetic field due to a wire of finite length first.
The Biot-Savart law gives the magnetic field contribution from a small circuit element ![]() carrying current
carrying current ![]() , at a point
, at a point ![]() away from it:
away from it:
(1) ![]()
To find the field generated by a straight wire, we break it up into small segments ![]() as shown in the figure. We are interested in the field at a point
as shown in the figure. We are interested in the field at a point ![]() away from the middle of the wire. Using the right hand rule,
away from the middle of the wire. Using the right hand rule,
(2) ![]()
which points into the plane of the paper. Therefore, the field due to the differential element ![]() is
is
(3) ![]()
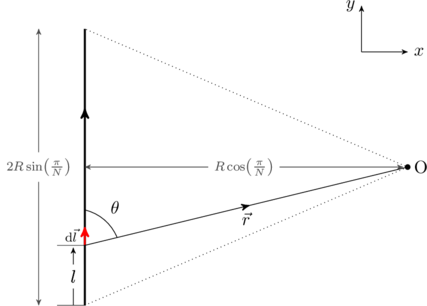
We can also find the following relationship between different lengths from the above figure,
(4) ![]()
Differentiating this leads us to a relationship between ![]() and
and ![]() ,
,
(5) ![]()
where we have used ![]() in the last step (another way of deriving the above relation is discussed at the end). Plugging this into (3),
in the last step (another way of deriving the above relation is discussed at the end). Plugging this into (3),
(6) ![]()
Integrating this expression gives the magnetic field due to a single side of the polygon at its center,
(7) ![]()
The total field at the center is
(8) ![]()
In the limit of large ![]() , the angle
, the angle ![]() becomes very small and we can approximate
becomes very small and we can approximate ![]() (see figure). Then,
(see figure). Then,
(9) ![]()
which is the field generated by a ring of current of radius ![]() , at its center.
, at its center.

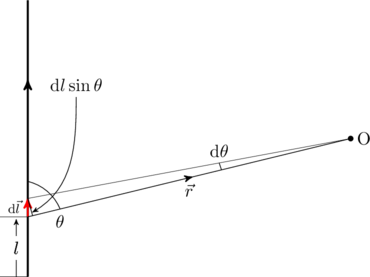
Note: We could also have related the differential length ![]() to
to ![]() with geometry (see figure),
with geometry (see figure),
(10) ![]()
Substituting ![]() leads us to (5).
leads us to (5).
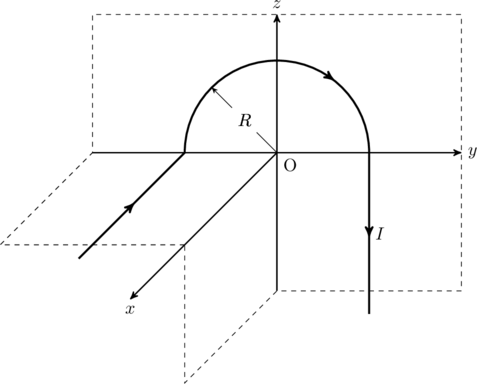
Bonus problem
Find the magnetic field at point O in the figure below.