JEE Advanced 2019 Paper 1, Question 8
A charged shell of radius ![]() carries a total charge
carries a total charge ![]() . Given
. Given ![]() as the flux of electric field through a closed cylindrical surface of height
as the flux of electric field through a closed cylindrical surface of height ![]() , radius
, radius ![]()
and with its center same as that of the shell. Here, the center of the cylinder is a point on the axis of the cylinder which is equidistant from its top and bottom surfaces. Which of the following option(s) is/are correct?
[![]() is the permittivity of free space]
is the permittivity of free space]
- If
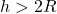 and
and  then
then 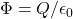
- If
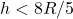 and
and 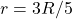 then
then 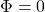
- If
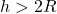 and
and 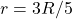 then
then 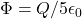
- If
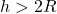 and
and 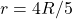 then
then 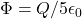
Related problems:
Electric field from a sphere …