JEE Advanced 2019 Paper 1, Question 8
A charged shell of radius ![]() carries a total charge
carries a total charge ![]() . Given
. Given ![]() as the flux of electric field through a closed cylindrical surface of height
as the flux of electric field through a closed cylindrical surface of height ![]() , radius
, radius ![]()
and with its center same as that of the shell. Here, the center of the cylinder is a point on the axis of the cylinder which is equidistant from its top and bottom surfaces. Which of the following option(s) is/are correct?
[![]() is the permittivity of free space]
is the permittivity of free space]
- If
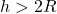 and
and  then
then 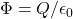
- If
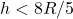 and
and 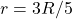 then
then 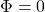
- If
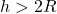 and
and 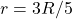 then
then 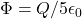
- If
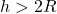 and
and 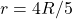 then
then 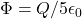
Related problems:
Electric field from a sphere with a cavity
Electric field in a hollow region
Charge at one corner of a cube
Electric flux through a hemisphere
Solution:
The cylinder in option (A) completely encloses the sphere, which means ![]() indeed by Gauss’s law.
indeed by Gauss’s law.
With a little geometry we can see that the cylinder in option (B) is contained within the sphere as shown below. Therefore the charge enclosed by the cyclinder is 0, which means ![]() .
.

The cylinder in option (C) contains a portion of the charged sphere as shown below (the angle ![]() ). The charge enclosed is
). The charge enclosed is

(1) ![]()
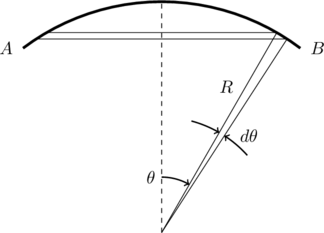
We can compute the area of ![]() (which is also the same as that of
(which is also the same as that of ![]() ) as shown in the figure below. Consider the shaded ring like segment of the region
) as shown in the figure below. Consider the shaded ring like segment of the region ![]() which subtends an angle
which subtends an angle ![]() at the center of the sphere. The radius of this ring is
at the center of the sphere. The radius of this ring is ![]() and its width is
and its width is ![]() . Its area is therefore
. Its area is therefore ![]() . The total area of
. The total area of ![]() is obtained by adding together the area of several such rings starting from
is obtained by adding together the area of several such rings starting from ![]() upto
upto ![]() . That is,
. That is,
(2) ![]()
The charge enclosed by the cylinder is therefore
(3) ![]()
where, in the last step we’ve substituted ![]() . Therefore, option (C) is correct.
. Therefore, option (C) is correct.
Finally, the cylinder in option (D) encloses more area of the sphere and so ![]() which means (D) is incorrect.
which means (D) is incorrect.
The correct answers are (A), (B), (C).