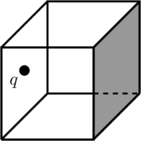
A charge ![]() sits at one corner of a cube of side length
sits at one corner of a cube of side length ![]() as shown in the figure below. What is the electric flux through the shaded side?
as shown in the figure below. What is the electric flux through the shaded side?
Related problems:
Electric field from a sphere with a cavity
Electric field in a hollow region
Flux from a charged shell
Solution
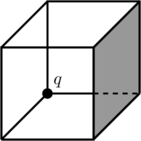
Since the problem is asking us to find the electric flux it is natural to guess that we need to apply Gauss’s Law. However, we need a closed surface with appropriate symmetry to be able to use Gauss’s Law (see article). So we consider the situation shown below.

We have placed the charge at the center of a cube of twice the side length as in the original problem. This is a closed surface, and by symmetry the flux though each side of the larger cube must be the same. To see why, imagine that top of the large cube, side ![]() , had a different flux through it than side
, had a different flux through it than side ![]() . If we tilt our head by
. If we tilt our head by ![]() in the clockwise direction, side
in the clockwise direction, side ![]() becomes the top face of the cube. But we still see a cube with a charge
becomes the top face of the cube. But we still see a cube with a charge ![]() at the center. That means the flux through the new top (side
at the center. That means the flux through the new top (side ![]() ) must be the same as the flux through the original top (side
) must be the same as the flux through the original top (side ![]() ). Repeating this argument, we see that the flux through each side will be the same.
). Repeating this argument, we see that the flux through each side will be the same.
We can now apply Gauss’s law,
(1) ![]()
where ![]() is the flux through each side. The electric field at different points on the side will be different. However, once again by symmetry we can see that the flux through the shaded region must be one-fourth of the flux through the side of the large cube. Thus,
is the flux through each side. The electric field at different points on the side will be different. However, once again by symmetry we can see that the flux through the shaded region must be one-fourth of the flux through the side of the large cube. Thus,
(2) ![]()
Bonus: Using the above technique, is it possible to calculate the flux through the shaded side if the charge were kept at the center of one of the opposite face?