IIT-JEE 2007 Paper 2, Question 6
(This problem is was repeated in JEE Advanced 2015 Paper 2, Question 11)
A spherical portion has been removed from a solid sphere having a charge distributed uniformly in its volume as shown in the figure. The electric field inside the emptied space is
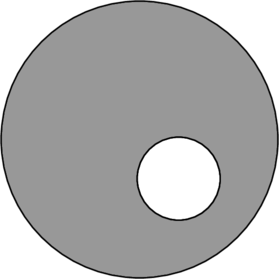
- zero everywhere
- non-zero and uniform
- non-uniform
- zero only at its center
Related Problems:
Electric field from a sphere with a cavity
Flux from a charged shell
Charge at one corner of a cube
Solution
As explained in a related problem we can think of the given charge distribution as a superposition of two spheres as shown below.
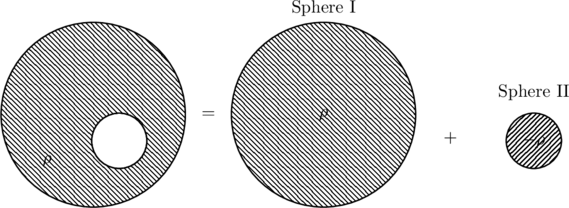
We can use this to determine the electric field at an arbitrary point (marked ![]() ) inside the hollow region (see figure).
) inside the hollow region (see figure).
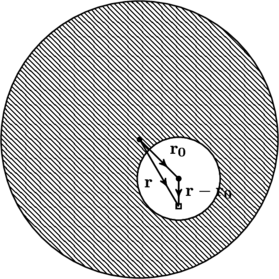
Recall that the electric field at a point within a sphere of uniform charge density ![]() is
is
(1) ![]()
which can be seen easily by applying Gauss’s law. Using this formula, the electric field at the point ![]() due to sphere I and II are
due to sphere I and II are
(2) 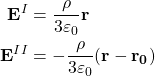
Adding these together, we find the net electric field
(3) ![]()
Notice that every symbol on the right hand side is a constant; ![]() is just the position of the center of the hollow region with respect to the center of the large sphere. That means the field at all points inside the hollow region is the same, or in other words it’s uniform! The field points in the
is just the position of the center of the hollow region with respect to the center of the large sphere. That means the field at all points inside the hollow region is the same, or in other words it’s uniform! The field points in the ![]() direction everywhere inside the hollow.
direction everywhere inside the hollow.
Bonus problem: Imagine that the figure above shows the cross-section of a long cylindrical rod carrying current of density ![]() out of the plane of the paper. A cylidrical cavity of arbitrary radius has been hollowed out as shown. Show that the magnetic field inside the hollow is uniform (in both magnitude and direction).
out of the plane of the paper. A cylidrical cavity of arbitrary radius has been hollowed out as shown. Show that the magnetic field inside the hollow is uniform (in both magnitude and direction).