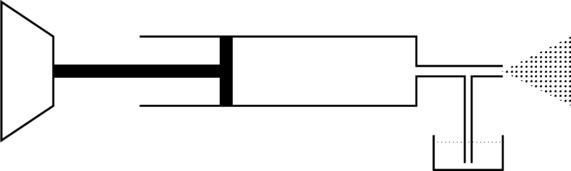
JEE Advanced 2013 Paper 1, Question 12
A solid sphere of radius ![]() and density
and density ![]() is attached to one end of a mass-less spring of force constant
is attached to one end of a mass-less spring of force constant ![]() . The other end of the spring is connected to another solid sphere of radius
. The other end of the spring is connected to another solid sphere of radius ![]() and density
and density ![]() . The complete arrangement is placed in a liquid of density
. The complete arrangement is placed in a liquid of density ![]() and is allowed to reach equilibrium. The correct statement(s) is (are)
and is allowed to reach equilibrium. The correct statement(s) is (are)
- the net elongation of the spring is
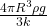 .
. - the net elongation of the spring is
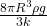
- the light sphere is partially submerged.
- the light sphere is completely submerged.
Solution
Recall that the buoyant force experienced by …