Archimedes’ principle with worked examples

This article reviews Archimedes’ principle and elaborates on the idea with three fully solved examples. The reader is encouraged to attempt the problems on their own before checking the solution.

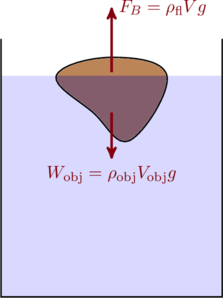
Consider a container $A$ of fluid at rest, as shown in the figure below. Since the fluid is at rest the net force on any part of the fluid is zero. Let us draw an imaginary boundary around some region of the fluid, as shown in the figure. This parcel of fluid has a weight $\rho_{\rm fl} V g$ , where $\rho_{\rm fl}$ is the density of the fluid and $V$ is the volume of the parcel. The parcel does not fall through the fluid under its weight because the fluid around the parcel exerts an upward force, called the buoyant force $F_B$ , on the parcel which counteracts its weight. That is, $F_B = \rho_{\rm fl} V g$ .

Rendered by QuickLaTeX.com

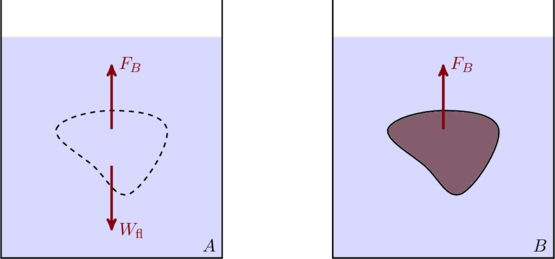
Now imagine we somehow swap out the parcel of liquid with an object of exactly the same shape and size, as in container $B$ . The surrounding fluid is not affected by what is inside the parcel, which means it exerts the same buoyant force on it as before. This is Archimedes principle:

The buoyant force on an object equals the weight of the fluid it displaces,

(1) $\begin{equation*} F_B = \rho_{\rm fl} V g . \end{equation*}$

What about the weight of the object in container $B$ ? There are three possibilities, depending on how the average density of the object $\rho_{\rm obj}$ compares to that of the fluid, $\rho_{\rm fl}$ :

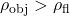$\rho_{\rm obj} > \rho_{\rm fl}$ : The object is heavier than the parcel of fluid it displaces since 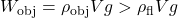$W_{\rm obj} = \rho_{\rm obj} V g > \rho_{\rm fl} V g$ . Therefore, 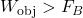$W_{\rm obj} > F_B$ and the object sinks to the bottom since the buoyant force is insufficient to hold it up.
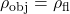$\rho_{\rm obj} = \rho_{\rm fl}$ : The buoyant force balances the weight of the object exactly, 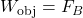$W_{\rm obj} = F_B$ , and the object remains fully submerged.
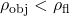$\rho_{\rm obj} < \rho_{\rm fl}$ : In this case a smaller volume of liquid needs to be displaced to balance the weight of the object, which means the object is only partially submerged (that is, it floats) as shown in figure. Then,

(2) $\begin{equation*} W_{\rm obj} = F_B \implies \rho_{\rm obj} V_{\rm obj} g = \rho_{\rm fl} V g \end{equation*}$

where $V_{\rm obj}$ is the total volume of the object, and $V$ is the volume of its submerged portion, which is also the volume of the liquid it displaces.

With that, we can move on to discuss some examples.

Example 1: Suspended between oil and water

(a) An object of uniform density is placed in a vessel containing water and oil as shown in the figure below. The object is suspended between the two liquids such that three quarters of its volume is submerged in water and the rest is in contact with the oil. What is the density of the object? Use $\rho_{\rm oil} = 0.8 {\rm g/cm}^3$ and $\rho_{\rm water} = 1 {\rm g/cm}^3$ .

Rendered by QuickLaTeX.com

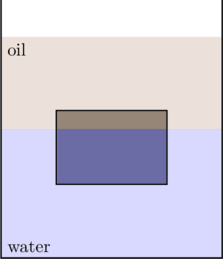
Solution: Using Archimedes’ principle the buoyant force is

(3) $\begin{equation*} F_B = \rho_{\rm oil} \frac{V_{\rm obj}}{4} g + \rho_{\rm water} \frac{3 V_{\rm obj}}{4} g . \end{equation*}$

Since the object does not touch the bottom of the vessel its weight $\rho_{\rm obj} V_{\rm obj} g$ must equal $F_B$ . This leads us to conclude

(4) $\begin{equation*} \rho_{\rm obj} = \frac{\rho_{\rm oil}}{4} + \frac{3 \rho_{\rm water}}{4} = 0.95 \, {\rm g/cm}^3. \end{equation*}$

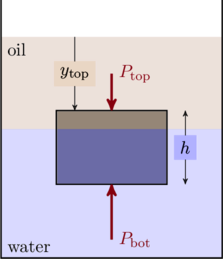
(b) In the preceding discussion we argued that the buoyant force is an upward force exerted by the fluid on the object. So here is a question: if there is no oil beneath the object, how does it exert a force on the object in the upward direction?

Solution: The oil exerts force on the object by applying its own weight on the water. To see this explicitly we can take examine the origin of the buoyant force from a slightly different perspective. We know that the pressure on the top face of the object is $P_{\rm top} = \rho_{\rm oil} y_{\rm top} g$ and that at the bottom face is $P_{\rm bot} = P_{\rm top} + \rho_{\rm oil} \frac{h}{4} g + \rho_{\rm water} \frac{3h}{4} g$ (see figure below). Since the object has a uniform cross-sectional area $A$ throughout we find the net upward force to be

(5) $\begin{equation*} F_B = (P_{\rm bot} - P_{\rm top}) A = \left( \frac{1}{4} \rho_{\rm oil} g + \frac{3}{4} \rho_{\rm water} g \right) \underbrace{(A h)}_{V_{\rm obj}} . \end{equation*}$

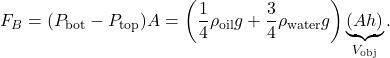
This is just the buoyant force we found in (3). But now we understand how the pressure from the oil manifests as an upward force on the object. If the same object were placed in a vessel with water alone, $95 \%$ of it’s volume would be below the water surface, whereas with oil present only $75 \%$ of the object is submerged in water.

Rendered by QuickLaTeX.com

Example 2: Melting ice

(a) A block of ice floats in a vessel containing water. After a while the ice completely melts. The water level in the vessel will

rise
fall
remain the same

Solution: The weight of the ice must be the same as the weight of liquid displaced, $\rho_{\rm ice} V_{\rm ice} g = \rho_{\rm water} V_{\rm water} g$ . When the ice melts it turns into water with volume $V = M_{\rm ice}/\rho_{\rm water} = \rho_{\rm ice} V_{\rm ice}/\rho_{\rm water}$ . In other words, it fills up exactly the volume that the ice had displaced before it melted. So the water level remains the same.

(b) A similar ice cube floats in a vessel containing salt water. When the ice melts completely, the water level will (Hint: Salt water is denser than pure water.)

rise
fall
remain the same

Solution: Here we have $\rho_{\rm ice} V_{\rm ice} g = \rho_{\rm salt-water} V_{\rm salt-water} g$ . However, the ice melts into a volume $V = \rho_{\rm ice} V_{\rm ice}/\rho_{\rm pure-water}$ . Since $\rho_{\rm pure-water} < \rho_{\rm salt-water}$ , we find $V > V_{\rm salt-water}$ which means the water level rises. This is why sea levels rise due to melting of the polar ice caps — the ice is mostly pure water whereas the ocean is salinated.

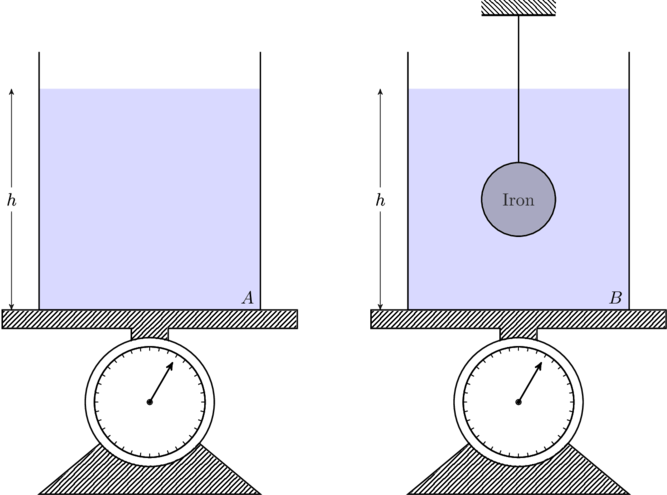
Example 3: The weight of buoyancy

(a) Two identical beakers rest on weight scales and are filled with water. Beaker $B$ has an iron sphere submerged in it, that is also connected to the ceiling by a taut string as shown in the figure. The water level $h$ is the same in both beakers. If the scales measure weights $W_A$ and $W_B$ , which of the following is true?

Rendered by QuickLaTeX.com

$W_A < W_B$
$W_A > W_B$
$W_A = W_B$

Solution: The volume of the water $V$ displaced by the iron sphere in $B$ exerts an upward buoyant force $F_B = \rho_{\rm water} V g$ on the sphere. The remaining force to hold the sphere in place comes from the tension of the string. By Newton’s law the reaction to $F_B$ is exerted on the liquid, and becomes part of weight we read off from the scale. But this is the same weight we would read off from $A$ since the volume $V$ in that case is filled with water itself. So $W_A = W_B$ .

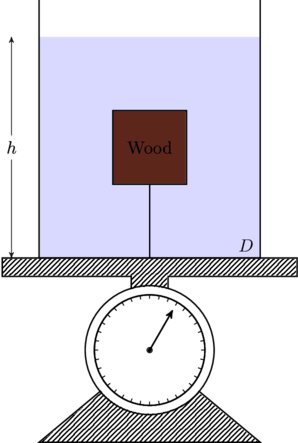
(b) Next, a wooden block floats in a similar beaker, call it $C$ , such that the water level is still $h$ . How does the weight $W_C$ compare with $W_A$ from the previous problem?

Rendered by QuickLaTeX.com

$W_A < W_C$
$W_A > W_C$
$W_A = W_C$

Solution: The scale reads the weight of the water plus the weight of the wooden block. That is, $W_C = \rho_{\rm water} V' g + W_{\rm block}$ , where $V'$ is the volume of water in the beaker. But the weight of the block is balanced by the buoyant force exterted by water on the block, which is nothing by the weight $\rho_{\rm water} V g$ of the displaced water ( $V$ is the volume of the block below the water surface). Therefore $W_C = \rho_{\rm water} (V'+V) g$ . In beaker $A$ we can imagine a parcel of water of volume $V$ in place of the submerged part of the block in $C$ . This tells us $W_A = \rho_{\rm water} (V'+V) g \equiv W_C$ .

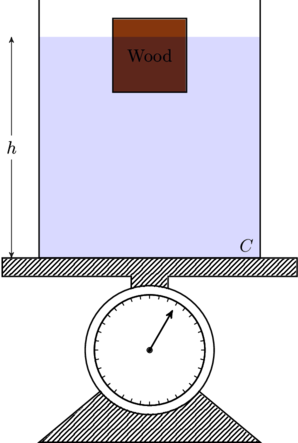
(c) Finally, a wooden block is tied down to bottom of the beaker $D$ , such that the water level is $h$ . How does the weight $W_D$ compare with $W_A$ ?

Rendered by QuickLaTeX.com

$W_A < W_D$
$W_A > W_D$
$W_A = W_D$

Solution: If the volume occupied by the wooden block were filled with water, as in $A$ the total contents of the beaker would be heavier. That means $W_A > W_D$ . The tension $T$ in the string makes up for the excess upward force so that $T = \rho_{\rm water} V g - W_{\rm block}$ .

Example 1: Suspended between oil and water

Example 2: Melting ice

Example 3: The weight of buoyancy

Leave a Reply Cancel reply