Bernoulli’s principle in a spray gun

JEE Advanced 2014 Paper 2, Questions 13 and 14

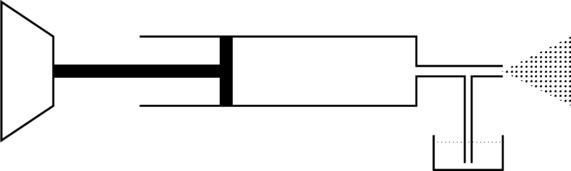
A spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are $20 {\rm~mm}$ and $1 {\rm~mm}$ , respectively. The upper end of the container is open to the atmosphere.

Rendered by QuickLaTeX.com

Q.1 If the piston is pushed at a speed of $5 {\rm ~mm \, s^{-1}}$ , the air comes out of the nozzle with a speed of

$0.1 {\rm ~m \, s^{-1}}$
$1 {\rm ~m \, s^{-1}}$
$2 {\rm ~m \, s^{-1}}$
$8 {\rm ~m \, s^{-1}}$

Q.2 If the density of air is $\rho_{\rm air}$ and that of the liquid $\rho_{\ell}$ , then for a given piston speed the rate (volume per unit time) at which the liquid is sprayed will be proportional to

$\sqrt{\frac{\rho_{\rm air}}{\rho_{\ell}}}$
$\sqrt{\rho_{\rm air} \rho_{\ell}}$
$\sqrt{\frac{\rho_{\ell}}{\rho_{\rm air}}}$
$\rho_{\ell}$

Solution

Q.1 Consider the points labelled $a$ , $b$ and $c$ in the figure below. Under the assumption that air is incompressible, the volume of air flowing through the cross section of the piston at point A must be the same as that flowing through point $b$ in the nozzle. That is,

(1) $\begin{equation*} v_a A_a = v_b A_b \implies v_b = v_a \frac{A_a}{A_b} = v_a \left( \frac{r_a}{r_b} \right)^2 \end{equation*}$

At point $c$ some liquid enters the air stream, but this does not change the volume available to air by that much since the liquid droplets occupy very little volume compared to air. Therefore, we can safely assume that the velocity of air leaving the nozzle is still $v_b$ ,

(2) $\begin{equation*} v_b = 5 \times 10^{-3} {\rm ~m \, s^{-1}} \left( \frac{20 {\rm ~mm}}{1 {\rm ~mm}} \right)^2 = 2 {\rm ~m \, s^{-1}} . \end{equation*}$

Therefore, option (C) is correct.

Rendered by QuickLaTeX.com

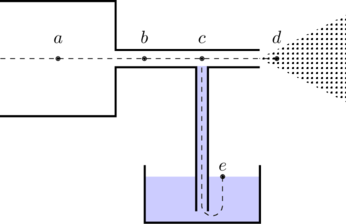
Q.2 Let’s take a moment to understand how the spray gun works. We’ve already established that air is flowing faster in the nozzle than in the piston. By the same reasoning (conservation of volume flow rate) the air-water mixture slows down as it expands into the atmosphere at point $d$ , which means $v_c > v_d$ . In fact, just outside the nozzle the spray nearly comes to a halt, so we can take $v_d \approx 0$ . We should ask ourselves the following question now: how is the pressure $P_c$ at point $c$ related the atmospheric pressure $P_{\rm atm}$ at point $d$ ?

To answer this, recall Bernoulli’s equation which tells us

(3) $\begin{equation*} P + \frac{1}{2} \rho v^2 + \rho g h = {\rm const.} \end{equation*}$

along a streamline of fluid. In particular, if the height of the fluid does not change (for example, along the line $bd$ in the figure above), the quantity $P + \frac{1}{2} \rho v^2$ must be conserved along the flow. This means

(4) $\begin{equation*} P_c + \frac{1}{2} \rho_{\rm air} v_c^2 = P_{\rm atm} + \frac{1}{2} \rho_{\rm air} v_d^2 \overset{v_c > v_d}{\implies} P_c < P_{\rm atm} . \end{equation*}$

That is, pressure is lower at the $c$ where air is moving faster. Consequently, the liquid in the container is pushed toward $c$ by the atmospheric pressure on its surface. The volumetric rate at which the liquid is sprayed is proportional to the velocity $u_c$ with which the liquid enters the air stream at point $c$ (we will use the letter $u$ to denote the velocity of the liquid, to avoid confusion with the velocity of air). Applying Bernoulli’s equation to the streamline $ec$ ,

(5) $\begin{equation*} P_c + \frac{1}{2} \rho_{\ell} u_c^2 + \rho_{\ell} g h_c = P_{\rm atm} + \frac{1}{2} \rho_{\ell} u_e^2 + \rho_{\ell} g h_e \end{equation*}$

If the liquid container is much wider than the tube the cross-sectional area $A_e$ of the liquid at $e$ is much larger than that at $c$ , which means $u_e = u_c A_c/A_e \ll u_c$ . Therefore we can ignore the $\frac{1}{2} \rho_{\ell} u_e^2$ term on the r.h.s. Furthermore, we can solve (4) with $v_d \approx 0$ to find $P_{\rm atm} - P_c = \frac{1}{2} \rho_{\rm air} v_c^2$ . Putting these relations in (5) we find

(6) $\begin{equation*} \frac{1}{2} \rho_{\ell} u_c^2 = \frac{1}{2} \rho_{\rm air} v_c^2 - \rho_{\ell} g (h_c - h_e) \implies u_c = \sqrt{\frac{\rho_{\rm air}}{\rho_{\ell}} v_c^2 - g(h_c-h_e)} . \end{equation*}$

This solution is real only if $v_c^2 > \frac{\rho_{\ell}}{\rho_{\rm air}} g(h_c-h_e)$ . Since the liquid is much denser than air, we need a large $v_c$ to satisfy this condition, which is why the piston has be so much bigger than the nozzle. It would also help to have the liquid container close to the nozzle so that $h_c-h_e$ is small. If $v_c$ is large enough, we can ignore the second term under the square root and write

(7) $\begin{equation*} u_c \approx \sqrt{\frac{\rho_{\rm air}}{\rho_{\ell}}} v_c , \end{equation*}$

and therefore the rate at which liquid is sprayed is proportional to $\sqrt{\frac{\rho_{\rm air}}{\rho_{\ell}}}$ . So option (A) is correct.

Leave a Reply Cancel reply