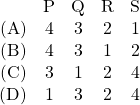
JEE Advanced 2017 Paper 2, Question 16, 17 and 18
An ideal gas is undergoing a cyclic thermodynamic process in different ways as shown in the corresponding ![]() diagrams in column 3 of the table. Consider only the path from state 1 to state 2.
diagrams in column 3 of the table. Consider only the path from state 1 to state 2. ![]() denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamic processes. Here
denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamic processes. Here ![]() is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is
is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is ![]() .
.
Related Article:…