Ideal gas match list

JEE Advanced 2017 Paper 2, Question 16, 17 and 18

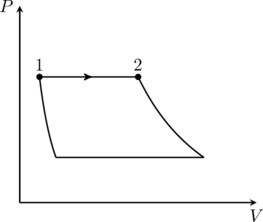
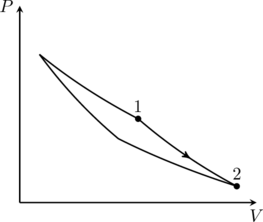
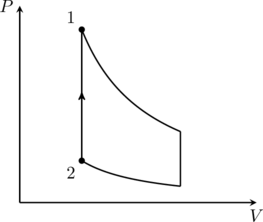
An ideal gas is undergoing a cyclic thermodynamic process in different ways as shown in the corresponding $P-V$ diagrams in column 3 of the table. Consider only the path from state 1 to state 2. $W$ denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamic processes. Here $\gamma$ is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is $n$ .

Related Article: Thermodynamic processes on an ideal gas

Column 1	Column 2	Column 3
(I) $W_{1 \rightarrow 2}=\frac{1}{\gamma-1}\left(P_{2} V_{2}-P_{1} V_{1}\right)$ 1	(i) Isothermal	(P)
(II) $W_{1 \rightarrow 2}=-P V_{2}+P V_{1}$	(ii) Isochoric	(Q)
(III) $W_{1 \rightarrow 2}=0$	(iii) Isobaric	(R)
(IV) $W_{1 \rightarrow 2}=-n R T \ln \left(\frac{V_{2}}{V_{1}}\right)$	(iv) Adiabatic	(S)

1. Which of the following options is the only correct representation of a process in which $\Delta U=\Delta Q-P \Delta V$ ?

(II) (iv) (R)
(III) (iii) (P)
(II) (iii) (S)
(II) (iii) (P)

2. Which one of the following options is the correct combination?

(IV) (ii) (S)
(III) (ii) (S)
(II) (iv) (P)
(II) (iv) (R)

3. Which one of the following options correctly represents a thermodynamic process that is used as a correction in the determination of the speed of sound in an ideal gas?

(I) (ii) (Q)
(IV) (ii) (R)
(III) (iv) (R)
(I) (iv) (Q)

Solution

1. By the first law of thermodynamics, an ideal gas satisfies $\Delta U = \Delta Q - P \Delta V$ . However, depending on the kind of process some of the terms in this equation may be zero. For the processes listed in column 2, we have

Isothermal	$\Delta U = 0 \implies \Delta Q - P \Delta V = 0$
Isochoric	$\Delta V = 0 \implies \Delta U = \Delta Q$
Isobaric	$\Delta P = 0 \implies \Delta U = \Delta Q - P \Delta V \checkmark$
Adiabatic	$\Delta Q = 0 \implies \Delta U = - P \Delta V$ .

So the process we are looking for is isobaric/constant pressure. The only diagram in column 3 with such a process is the first one, (P). Next, the work done on the gas in an isobaric process is

(1) $\begin{equation*} W_{1 \to 2} = - \int_{V_1}^{V_2} P {\rm d} V = -P(V_2-V_1), \end{equation*}$

since the pressure $P$ is constant. This is (II) from column 1. We conclude that that option (D) is correct. Note the sign of $W$ in (1) — since the gas is expanding from $1 \to 2$ in (P), $V_2 > V_1$ , which means the work done on the gas is negative (see note).

2. This problem asks us to match of the entries in the three columns. The correct combinations are (I)(iv)(Q), (II)(iii)(P), (III)(ii)(S), (IV)(iii)(R). The explanations for these are given here. Only option (B) matches one of these, and therefore option (B) is correct.

3. Laplace corrected Newton’s formula for the velocity of sound in a gas by assuming that the pressure-volume changes that occur when sound propagates through the gas is adiabatic. This corresponds to the sequence (I)(iv)(Q) in the given table. Therefore option (D) is correct.

Leave a Reply Cancel reply