Electric flux through a hemisphere

JEE Advanced 2017 Paper 2, Question 10

A point charge $+Q$ is placed just outside an imaginary hemispherical surface of radius ${\rm R}$ as shown in the figure. Which of the following statements is/are correct?

Rendered by QuickLaTeX.com

The electric flux passing through the curved surface of the hemisphere is $-\frac{Q}{2 \varepsilon_{0}}\left(1-\frac{1}{\sqrt{2}}\right)$
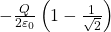
Total flux through the curved and the flat surfaces is $\frac{Q}{\varepsilon_{0}}$
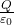
The component of the electric field normal to the flat surface is constant over the surface
The circumference of the flat surface is an equipotential

Solution

In problems like these a beginner may try to find the flux by integrating the electric field over the hemispherical surface. This would involve finding the normal component of the electric field on each differential area element of that surface, and integrating the resulting expression over the whole hemisphere. Such a calculation is time consuming and unnecessary. We can arrive at the answer much quicker by noticing that the net flux through the curved surface must the same as the flux leaving the flat surface, as shown in the figure below.

Rendered by QuickLaTeX.com — The next flux entering the curved part is the same as the flux leaving the flat part. The blue lines represent the electric field.

The hemisphere and its base form a closed surface, call it $S$ , when taken together. But this surface does not enclose any charge. Therefore, by Gauss’s law

(1) $\begin{equation*} \oint_S {\bf E} \cdot {\rm d} {\bf a} = 0 \implies \int_{\rm h.s.} {\bf E} \cdot {\rm d} {\bf a} + \int_{\rm base} {\bf E} \cdot {\rm d} {\bf a} = 0 . \end{equation*}$

where, in the second step, we have split the surface integral over $S$ into integrals over the hemisphere ( ${\rm h.s}$ ) and the base. It is clear from above that option (B) is incorrect. We can just find the flux through the base and take its negative to check option (A). To find this flux we note that the base subtends a solid angle around $+Q$ ,

(2) $\begin{equation*} \Omega_{\rm base} = \int_0^{2\pi} {\rm d} \phi \int_0^{\pi/4} {\rm d} \theta \sin \theta = 2 \pi \left( 1 - \frac{1}{\sqrt{2}} \right) . \end{equation*}$

Therefore, the total flux through the base is

(3) $\begin{equation*} \int_{\rm base} {\bf E} \cdot {\rm d} {\bf a} = \frac{\Omega_{\rm base}}{4 \pi} \times \frac{Q}{\varepsilon_0} = \frac{Q}{2 \varepsilon_{0}}\left(1-\frac{1}{\sqrt{2}}\right) . \end{equation*}$

By (1), the flux through the hemispherical part is

(4) $\begin{equation*} \int_{\rm h.s.} {\bf E} \cdot {\rm d} {\bf a} = -\frac{Q}{2 \varepsilon_{0}}\left(1-\frac{1}{\sqrt{2}}\right) % \implies % \text{\bf option (A) is correct} . \end{equation*}$

whch means option (A) is correct. Furthermore, the electric field normal to the base is

(5) $\begin{equation*} {\bf E}_\perp = - E \cos \theta \hat{\bf z} = - \frac{1}{4 \pi \varepsilon_0} \frac{Q}{R^2 + x^2} \frac{R}{\sqrt{R^2 + x^2}} \hat{\bf z} , \end{equation*}$

which clearly depends on the distance $x$ from the center of the base (see figure below). So option (C) is incorrect.

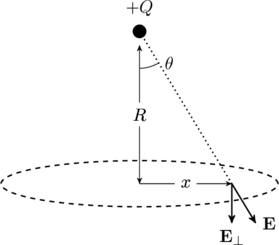
It is also clear from this figure that all points at the circumference of the base are equidistant from the charge $+Q$ . Therefore the circumference is indeed an equipotential, and option (D) is correct.

Leave a Reply Cancel reply