IIT-JEE 2008 Paper 1, Question 38,39,40
A small spherical monoatomic ideal gas bubble ![]() is trapped inside a liquid of density
is trapped inside a liquid of density ![]() (see figure below). Assume that the bubble does not exchange any heat with the liquid. The bubble contains
(see figure below). Assume that the bubble does not exchange any heat with the liquid. The bubble contains ![]() moles of gas. The temperature of the gas when the bubble is at the bottom is
moles of gas. The temperature of the gas when the bubble is at the bottom is ![]() , the height of the liquid is
, the height of the liquid is ![]() and the atmospheric pressure is
and the atmospheric pressure is ![]() (Neglect surface tension).
(Neglect surface tension).

1. As the bubble moves upwards, besides the buoyancy force the following forces are acting on it
- Only the force of gravity
- The force due to gravity and the force due to the pressure of the liquid
- The force due to gravity, the force due to the pressure of the liquid and the force due to viscosity of the liquid
- The force due to gravity and the force due to viscosity of the liquid
2. When the gas bubble is at a height ![]() from the bottom, its temperature is
from the bottom, its temperature is
3. The buoyancy force acting on the gas bubble [at height ![]() ] is (assume
] is (assume ![]() is the universal gas constant)
is the universal gas constant)
Solutions
1. There are three forces acting on the bubble: the force of gravity acting on the air inside the bubble, the viscous force acting against the upward motion of the bubble, and the pressure exerted by the liquid on the bubble. The latter creates the upward buoyant force, which we are told to ignore, so the correct answer is (D).
2. For an adiabatic process, the temperature and pressure satisfy (see (19) of this note)
(1) 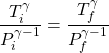
where ![]() and
and ![]() denote the initial and final values. When the bubble is at the very bottom of the container it has a temperature
denote the initial and final values. When the bubble is at the very bottom of the container it has a temperature ![]() , and it experiences pressure due to the surrounding liquid and the atmosphere above it. In practice, the pressure at different points on the bubble will be different and it will deform accordingly. But we’re told that the bubble is small and spherical, so we can take the pressure on it to be approximately constant,
, and it experiences pressure due to the surrounding liquid and the atmosphere above it. In practice, the pressure at different points on the bubble will be different and it will deform accordingly. But we’re told that the bubble is small and spherical, so we can take the pressure on it to be approximately constant, ![]() , when it is at the bottom. Similarly, when the bubble is at a height
, when it is at the bottom. Similarly, when the bubble is at a height ![]() from the bottom, the pressure is
from the bottom, the pressure is ![]() . Using \eqref{eq:AdiabaticTP}, the temperature at this height is
. Using \eqref{eq:AdiabaticTP}, the temperature at this height is
(2) 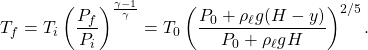
Therefore option (B) is correct.
3. The buoyant force ![]() exerted by the fluid is the weight of the fluid that was displaced. This is Archimedes’ principle. If we denote the volume of the bubble by
exerted by the fluid is the weight of the fluid that was displaced. This is Archimedes’ principle. If we denote the volume of the bubble by ![]() , the weight of the liquid that it displaces is
, the weight of the liquid that it displaces is ![]() . So, all we need to do is find
. So, all we need to do is find ![]() . Using (14) of this note,
. Using (14) of this note,
(3) 
The initial volume ![]() of the bubble, when it is at the bottom, can be determined by the ideal gas law,
of the bubble, when it is at the bottom, can be determined by the ideal gas law, ![]() ,
,
(4) ![]()
Plugging this into the previous equation, we find
(5) 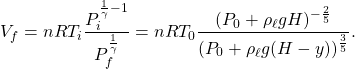
The buoyant force is therefore
(6) ![]()
in the upward direction. So option (B) is correct.