JEE Advanced 2019 Paper 1, Question 9
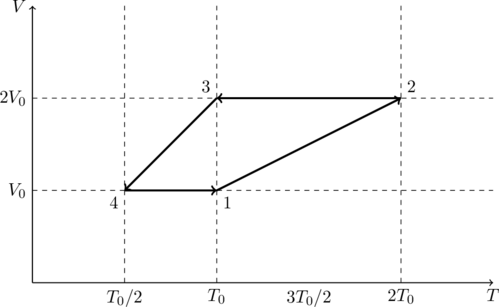
One mole of a monatomic ideal gas goes through a thermodynamic cycle, as shown in the volume vs. temperature (![]() ) diagram. The correct statement(s) is/are:
) diagram. The correct statement(s) is/are:
[![]() is the gas constant]
is the gas constant]
- Work done in this thermodynamic cycle (
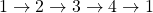 ) is
) is 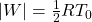 .
. - The above thermodynamic cycle exhibits only isochoric and adiabatic processes.
- The ratio of heat transfer during processes
 and
and 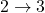 is
is 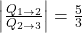 .
. - The ratio of heat transfer during processes
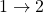 and
and 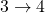 is
is 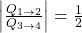 .
.
Related article: Thermodynamic processes on an ideal gas
Solution
An ideal gas obeys the relations
(1) ![]()
(2) ![]()
(3) ![]()
We are told that there is one mole of gas so ![]() . Let us draw a
. Let us draw a ![]() diagram for this process.
diagram for this process.
At point 4 we have ![]() and, by (1),
and, by (1), ![]() . From point
. From point ![]() the volume remains constant, however the temperature increases. That means
the volume remains constant, however the temperature increases. That means ![]() .
.
From point ![]() both volume and temperature increase in a linear fashion. That means the pressure must be constant. Therefore
both volume and temperature increase in a linear fashion. That means the pressure must be constant. Therefore ![]() and
and ![]() .
.
From ![]() there is no change in volume but the temperature drops. That means the pressure drops as well. So we have
there is no change in volume but the temperature drops. That means the pressure drops as well. So we have ![]() and by (1),
and by (1), ![]() .
.
Finally, from ![]() both volume and temperature decrease in a linear fashion, which means the pressure is a constant. So
both volume and temperature decrease in a linear fashion, which means the pressure is a constant. So ![]() ,
, ![]() and we have completed the cycle.
and we have completed the cycle.
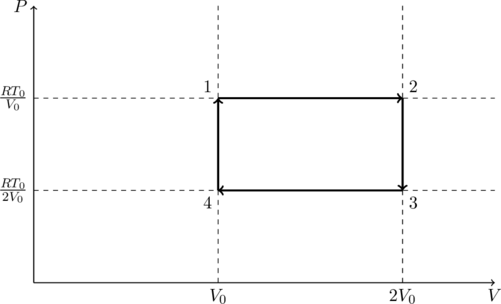
The work done by the gas is the area enclosed by the ![]() curve,
curve,
(4) ![]()
So option (A) is correct. It is also clear from the ![]() diagram that the cycle consists of only isobaric (constant pressure) and isochoric (constant volume) processes. So option (B) is incorrect.
diagram that the cycle consists of only isobaric (constant pressure) and isochoric (constant volume) processes. So option (B) is incorrect.
To compute the heat exchanged we recall the first law of thermodynamics,
(5) ![]()
We can compute ![]() from the
from the ![]() diagram using (3), and
diagram using (3), and ![]() from the
from the ![]() diagram using (2).
diagram using (2).
(6) ![Rendered by QuickLaTeX.com \begin{gather*} Q_{1 \to 2} = \Delta U_{1 \to 2} + \int_1^2 P dV = \frac{3}{2} R T_0 + R T_0 = \frac{5}{2} R T_0 \\[1em] Q_{2 \to 3} = \Delta U_{2 \to 3} + \int_2^3 P dV = -\frac{3}{2} R T_0 + 0 = -\frac{3}{2} R T_0 \\[1em] Q_{3 \to 4} = \Delta U_{3 \to 4} + \int_3^4 P dV = -\frac{3}{2} R T_0 -\frac{1}{2} R T_0 = -2 R T_0 \end{gather*}](https://www.jeefirst.com/wp-content/ql-cache/quicklatex.com-97845d2b83b04335333305073e088048_l3.png)
Therefore,
(7) ![]()
which means option (C) is correct. However,
(8) ![]()
and therefore option (D) is incorrect.
The correct answers are (A) and (C).