JEE Advanced 2019 Paper 1, Question 10
A thin convex lens is made of two materials with refractive indices ![]() and
and ![]() as shown in figure. The radius of curvature of the left and right spherical surfaces are equal.
as shown in figure. The radius of curvature of the left and right spherical surfaces are equal. ![]() is the focal length of the lens when
is the focal length of the lens when ![]() . The focal length is
. The focal length is ![]() when
when ![]() and
and ![]() . Assuming
. Assuming ![]() and
and ![]() , the correct statement(s) is/are,
, the correct statement(s) is/are,
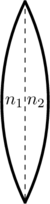
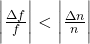
- For
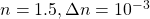 and
and 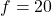 cm, the value of
cm, the value of 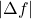 will be 0.02 cm (round off to
will be 0.02 cm (round off to 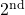 decimal place).
decimal place). - If
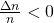 then
then 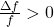
- The relation between
 and
and 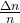 remains unchanged if both the convex surfaces are replaced by concave surfaces of the same radius of curvature.
remains unchanged if both the convex surfaces are replaced by concave surfaces of the same radius of curvature.
Related articles:
Lenses I: The thin lens equation
Lenses II: Image formation
Solution
(1) ![]()
where ![]() is the radius of curvature the object facing side (we keep the object on the left/front) and
is the radius of curvature the object facing side (we keep the object on the left/front) and ![]() is the radius of the other side. By convention,
is the radius of the other side. By convention, ![]() is positive when the center of curvature is in the back of the lens and negative otherwise. For instance, applying this convention to the lens in the figure below we can see that focal length of a convex lens is always positive. If the radii of the the two surfaces are equal in magnitude and
is positive when the center of curvature is in the back of the lens and negative otherwise. For instance, applying this convention to the lens in the figure below we can see that focal length of a convex lens is always positive. If the radii of the the two surfaces are equal in magnitude and ![]() , (1) gives
, (1) gives
(2) ![]()

When ![]() the lens can be thought of as two plano-convex lenses in series. The focal length of such an arrangement is
the lens can be thought of as two plano-convex lenses in series. The focal length of such an arrangement is
(3) ![]()
where the focal length of each plano-convex lens can be obtained using \eqref{eq:q10LensMaker} by setting one of the radii to ![]() , corresponding to the plane face. That is,
, corresponding to the plane face. That is,
(4) 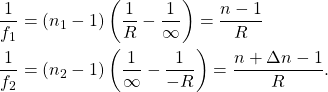
Substituting these in (3)
(5) 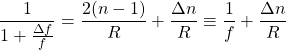
where we’ve set the effective focal length to ![]() as given in the problem. Multiplying both sides of this equation by
as given in the problem. Multiplying both sides of this equation by ![]() we get
we get
(6) ![]()
For a small change in refractive index between ![]() and
and ![]() , the change
, the change ![]() . Therefore we can expand the expression on the left side using
. Therefore we can expand the expression on the left side using ![]() for
for ![]() ,
,
(7) ![]()
To relate ![]() to
to ![]() , we note that
, we note that
(8) ![]()
since ![]() . That means
. That means ![]() , which implies
, which implies ![]() . Thus,
. Thus,
(9) ![]()
The relation between the absolute values of these ratios is more subtle. To see this note that (7) relates the sign of ![]() and
and ![]() (recall that
(recall that ![]() and
and ![]() are positive). For
are positive). For ![]() we have
we have ![]() and (9) implies
and (9) implies
(10) ![]()
On the other hand, if ![]() we have
we have ![]() , and (9) tells us
, and (9) tells us
(11) ![]()
So (A) is not always true, so we take that option to be incorrect. We also saw from this discussion that if ![]() then
then ![]() , which means (C) is correct.
, which means (C) is correct.
For ![]() and
and ![]() cm, (7) gives
cm, (7) gives ![]() cm. So option (B) is correct.
cm. So option (B) is correct.
Finally, changing both convex surfaces to concave simply changes ![]() in the equations above. While this changes the sign of
in the equations above. While this changes the sign of ![]() , it does not alter (7) which means the relation (9) between
, it does not alter (7) which means the relation (9) between ![]() and
and ![]() remains unaffected. So (D) is correct.
remains unaffected. So (D) is correct.
Thus, the correct answers are (B), (C) and (D).
Discussion
When the surfaces are concave ![]() and
and ![]() will have the same sign by (7), since
will have the same sign by (7), since ![]() . Does this change the relationship between the absolute values
. Does this change the relationship between the absolute values ![]() and
and ![]() ?
?