Doppler effect and beats

JEE Advanced 2019 Paper 1, Question 15

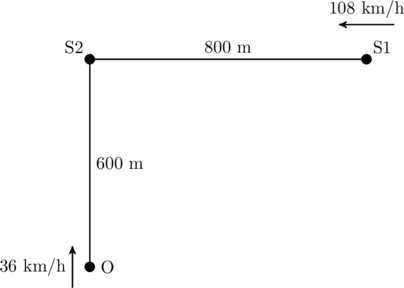
A train S1, moving with a uniform velocity of $108$ km/h, approaches another train S2 standing on a platform. An observer O moves with a uniform velocity of $36$ km/h towards S2, as shown in figure. Both the trains are blowing whistles of same frequency $120$ Hz. When $\mathrm{O}$ is $600$ m away from S2 and distance between $\mathrm{S} 1$ and $\mathrm{S} 2$ is $800$ m, what is the number of beats heard by O?

[Speed of the sound $=330$ m/s ]

Rendered by QuickLaTeX.com

Recommended reading: How does Doppler effect work?

Solution

When there is relative motion between the source and observer, the observed frequency $f_o$ is related to the source frequency $f_s$ by

(1) $\begin{equation*} f_O = \frac{v + v_O}{v-v_S} f_S , \end{equation*}$

where $v$ is the velocity of sound in the medium, $v_o$ is the velocity with which the observer moves towards the source, and $v_s$ is the velocity with which the source moves towards the observer. This is the equation for the Doppler Effect.

In the given problem both sources (the trains) emit sound with frequency $120$ Hz. The observer O hears sounds of frequencies

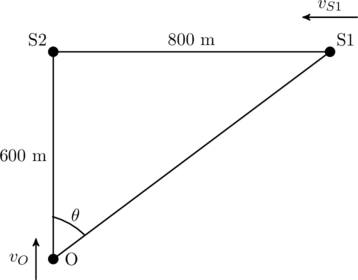
(2) $\begin{align*} f^{(1)}_O &= \frac{v+v_O \cos\theta}{v-v_{S1} \sin{\theta}} f_{S1} = \frac{336}{306} \times 120 \, {\rm Hz} , \\[1em] f^{(2)}_O &= f_{S2} = \frac{v+v_O}{v} = \frac{340}{330} \times 120 \, {\rm Hz} \end{align*}$

where the angle $\theta$ is indicated in the figure below and we have plugged in $v_O = 36$ km/h, $v_{S1} = 108$ km/h, $\cos \theta = \frac{3}{5}$ , and $\sin \theta = \frac{4}{5}$ .

Rendered by QuickLaTeX.com

The beat frequency is

(3) $\begin{equation*} \boxed{f_{\rm beats} = \left| f^{(1)}_O-f^{(2)}_O \right| = 0.81 \ {\rm beats/second} .} \end{equation*}$

Leave a Reply Cancel reply