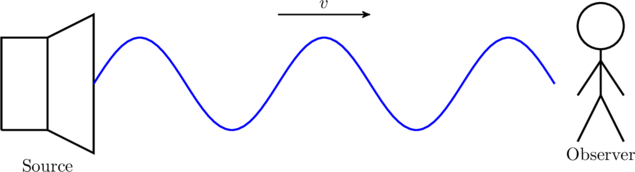
The Doppler effect for sound is a perceived difference between the frequency of sound heard by an observer and the actual frequency emitted by a source, due to relative motion between the source and the observer. A familiar example of this phenomenon is the change in sound frequency of an ambulance or fire engine as it rushes past you. We give a visual explanation of this effect and derive the relation between the observed and emitted frequencies below.
First, recall that the velocity of sound in a medium, ![]() , is a property of the medium alone. That is, after the wave has left the source it will always travel at velocity
, is a property of the medium alone. That is, after the wave has left the source it will always travel at velocity ![]() , irrespective of the motion of the source and/or observer. Let us now consider what happens in different scenarios, one by one.
, irrespective of the motion of the source and/or observer. Let us now consider what happens in different scenarios, one by one.
Case 0: The source and observer are both at rest. The source emits sound with frequency ![]() (period
(period ![]() ) and the wavelength of sound received by the observer is
) and the wavelength of sound received by the observer is ![]() . These quantities satisfy the relation
. These quantities satisfy the relation
(1) ![]()
which is the statement that one full wavelength ![]() leaves the stationary source in one time period
leaves the stationary source in one time period ![]() . Note that, we have represented sound waves by a sinusoidal shape in the diagram below. Sound waves are actually longitudinal, which means the compressions and rarefactions that make up the wave are aligned along the direction in which the wave propagates.
. Note that, we have represented sound waves by a sinusoidal shape in the diagram below. Sound waves are actually longitudinal, which means the compressions and rarefactions that make up the wave are aligned along the direction in which the wave propagates.
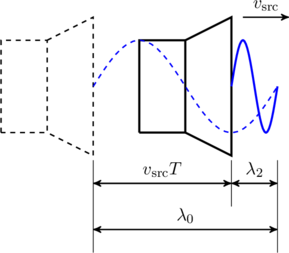
Case 1: The source travels at the same velocity as the sound it emits, that is ![]() . Then, the source catches up with the sound as it tries to leave and ultimately no sound is emitted from the source (see figure), which means
. Then, the source catches up with the sound as it tries to leave and ultimately no sound is emitted from the source (see figure), which means ![]() !
!

Case 2: The source travels at a velocity ![]() in the direction of the sound. In this case, the source catches up a little but sound is still emitted from the source at velocity
in the direction of the sound. In this case, the source catches up a little but sound is still emitted from the source at velocity ![]() . The figure below shows the source at its intial position (dashed) and after time
. The figure below shows the source at its intial position (dashed) and after time ![]() has elapsed. Clearly the wavelength
has elapsed. Clearly the wavelength ![]() is shorter; if we increase
is shorter; if we increase ![]() all the way up to
all the way up to ![]() , the wavelength
, the wavelength ![]() goes to zero as in the figure above.
goes to zero as in the figure above.

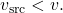
To determine ![]() , we consider what happens when one period of the wave has elapsed, that is
, we consider what happens when one period of the wave has elapsed, that is ![]() . As shown in the figure below, if the source were at rest a sound wave of length
. As shown in the figure below, if the source were at rest a sound wave of length ![]() (dashed) would have emanated from the source in this time. However, in this time the source has caught up by a distance
(dashed) would have emanated from the source in this time. However, in this time the source has caught up by a distance ![]() , and only a length
, and only a length ![]() of the wave ends up coming out of the source. Therefore, using (1)
of the wave ends up coming out of the source. Therefore, using (1)
(2) ![]()
Since ![]() , the frequency
, the frequency ![]() received by the observer will be greater than
received by the observer will be greater than ![]() , as shown in the figure above. If the source were moving in the opposite direction to the sound, we can still use (2), with a negative value of
, as shown in the figure above. If the source were moving in the opposite direction to the sound, we can still use (2), with a negative value of ![]() . In that case
. In that case ![]() , as you can verify by drawing diagrams similar to the ones above.
, as you can verify by drawing diagrams similar to the ones above.
Case 3: The observer moves toward the source (see figure). The wavelength of sound does not change in this scenario, however the frequency of sound heard by the observer does. How?
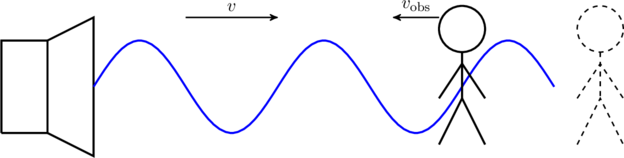
Once again we examine what happens in one time period ![]() . Consider the situation shown in the figure below. If the observer remained at their initial position (dashed), one whole wavelength would pass them in time
. Consider the situation shown in the figure below. If the observer remained at their initial position (dashed), one whole wavelength would pass them in time ![]() . However, since the observer chose to move toward the source an additional
. However, since the observer chose to move toward the source an additional ![]() length of the sound wave also passes through them. In other words more number of waves are received by the observer in any given window of time, due to their motion.
length of the sound wave also passes through them. In other words more number of waves are received by the observer in any given window of time, due to their motion.
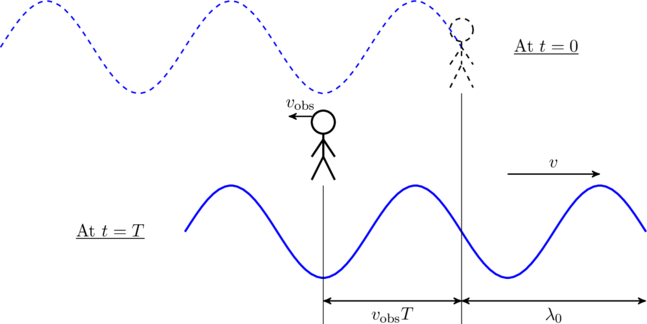
The number of waves (i.e. full wavelengths) encountered by the observer in one time period is just the observed frequency ![]() , given by
, given by
(3) ![]()
where we’ve used (1). As in case 2, if the observer is moving away from the source, we just need to use a negative value of ![]() to find the correct
to find the correct ![]() .
.
We may combine (2) and (3) to obtain the Doppler effect when both source and observer are moving,
(4) ![]()
where ![]() is positive if the source is moving toward the observer and
is positive if the source is moving toward the observer and ![]() is positive if the observer is moving toward the source.
is positive if the observer is moving toward the source.
Question: What happens when the source and observer are at rest, but there is a wind blowing? Using the same line of reasoning as above, find a formula relating the observed frequency to the emitted frequency. The answer may surprise you!
Related Problems:
A collection of Doppler effect problems
Doppler effect and beats