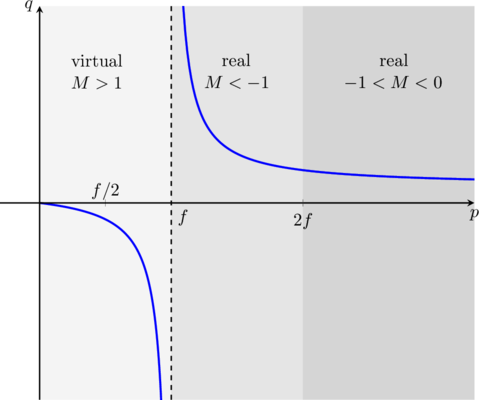
Continuing our discussion from the previous chapter, we can use the thin lens equation and our knowledge of the signs of ![]() , to determine the position, orientation, and magnification of the image for different object distances
, to determine the position, orientation, and magnification of the image for different object distances ![]() . This is similar to the analysis we did for mirrors here. The results are summarized in the table below.
. This is similar to the analysis we did for mirrors here. The results are summarized in the table below.
Converging lens
The focal length of a converging lens is positive. That means light from infinity will be brought to focus behind the lens. We will begin our analysis there.
Starting from ![]()
Consider an object kept in front of a converging lens. If the object is very far away, we take ![]() , which means
, which means ![]() . By the thin lens equation, the image will be at
. By the thin lens equation, the image will be at ![]() , as expected. If we gradually bring the object closer to the lens, such that
, as expected. If we gradually bring the object closer to the lens, such that ![]()
(1) ![]()
By the sign convention for lenses, this implies the image is behind the lens. Also recall that magification due to a lens or mirror is given by
(2) ![]()
where ![]() and
and ![]() are the heights of the image and the object repectively. Since the object is in front of the lens,
are the heights of the image and the object repectively. Since the object is in front of the lens, ![]() is positive, and by (1), so is
is positive, and by (1), so is ![]() . Therefore,
. Therefore,
(3) ![]()
which means the image is inverted. The image will be enlarged or shrunk down depending on whether ![]() or
or ![]() .
.
![]()
If the object is kept at some finite distance ![]() from the lens
from the lens
(4) ![]()
where, in the second step we used ![]() . Thefore, as the object is moved from
. Thefore, as the object is moved from ![]() to
to ![]() , the image moves between
, the image moves between ![]() and
and ![]() . The image is inverted, as discussed above, but we also find that it is smaller than the object,
. The image is inverted, as discussed above, but we also find that it is smaller than the object,
(5) ![]()
This is illustrated in the figure below. We can also arrive at the same conclusions by ray tracing.
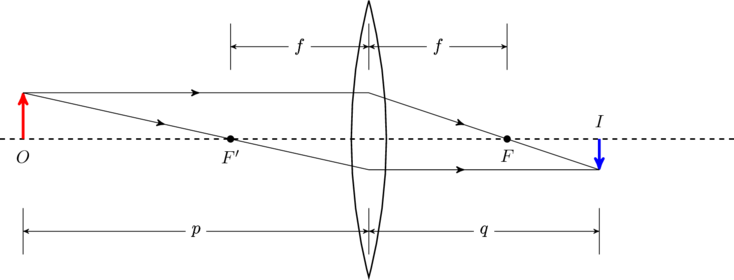
 . The image is inverted and smaller than the object.
. The image is inverted and smaller than the object.![]()
As the object is moved closer to the lens the image keeps moving farther away behind the lens. When ![]() gets closer than
gets closer than ![]() we find
we find
(6) ![]()
Therefore the image is larger than the object (see figure), since
(7) ![]()
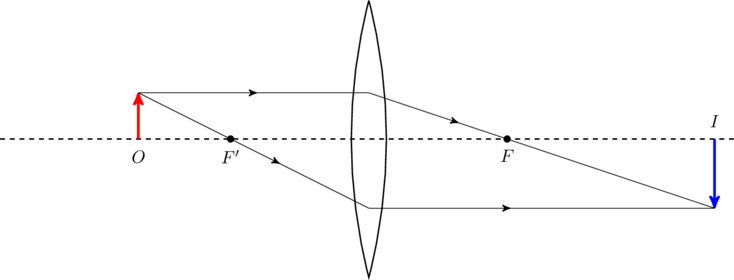
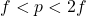 . The image is inverted and larger than the object.
. The image is inverted and larger than the object.Moving through ![]()
If the object is moved further towards the focal point ![]() , the image keeps moving further away till, for
, the image keeps moving further away till, for ![]() , the object forms at infinity behind the lens (the outgoing refracted rays are parallel to the optical axis). As we move the object past
, the object forms at infinity behind the lens (the outgoing refracted rays are parallel to the optical axis). As we move the object past ![]() , the image returns from infinity in front of the lens (we saw something similar happen with concave mirrors here). In other words, the image moves from
, the image returns from infinity in front of the lens (we saw something similar happen with concave mirrors here). In other words, the image moves from ![]() to
to ![]() as the object travels through
as the object travels through ![]() . The change in sign of
. The change in sign of ![]() (cf. (1)) can be seen from the thin lens equation,
(cf. (1)) can be seen from the thin lens equation,
(8) ![]()
We can be more precise. Solving the first equation above we find ![]() which also means
which also means
(9) ![]()
since ![]() . A positive
. A positive ![]() implies the image is upright, but more importantly the image is magnified since
implies the image is upright, but more importantly the image is magnified since ![]() . This is the basic principle behind a simple magnifier. Lastly, an image formed in front of the lens is always virtual as illustrated in this figure and this one.
. This is the basic principle behind a simple magnifier. Lastly, an image formed in front of the lens is always virtual as illustrated in this figure and this one.
![]()
When the object is placed at ![]() ,
,
(10) ![]()
That is, the image is to the left of ![]() (see figure).
(see figure).
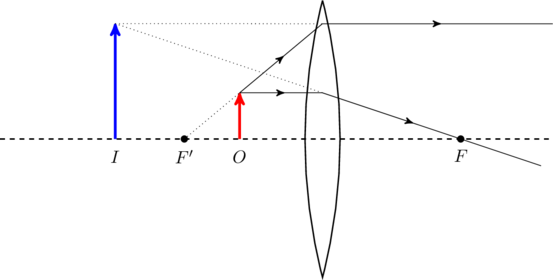
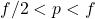 .
.![]()
As we continue moving the object closer to the lens the image moves closer as well (this is the opposite of what happens when ![]() ). If the object is brought closer than
). If the object is brought closer than ![]() ,
,
(11) ![]()
which means the image crosses ![]() . It is still magnified, but not quite as much as before (see figure). In fact, as the object approaches
. It is still magnified, but not quite as much as before (see figure). In fact, as the object approaches ![]() the image gets smaller till it is the same size as the object.
the image gets smaller till it is the same size as the object.
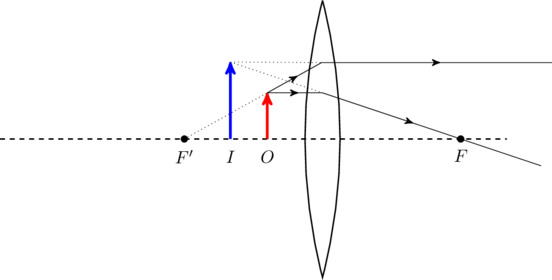
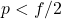 .
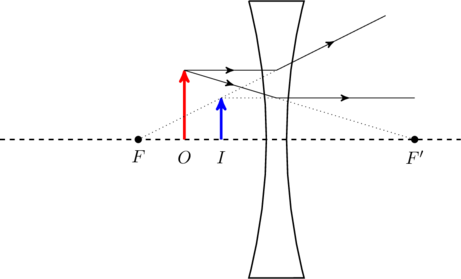
.Diverging lens
A diverging lens has negative focal length, which we may write as ![]() . Therefore
. Therefore
(12) ![]()
In other words, the image is always virtual, since it is appears in front of the lens. Furthermore,
(13) ![]()
That is, the magnification is a positive number smaller than 1, which means the image is upright and shrunk down in addition to being virtual. In fact, the image grows in size as we approach ![]() . This is illustrated in this figure and this one. Note that for a diverging lens the focal points
. This is illustrated in this figure and this one. Note that for a diverging lens the focal points ![]() and
and ![]() have been exchanged compared to a converging lens (see first chapter).
have been exchanged compared to a converging lens (see first chapter).

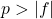 .
.
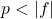 .
.Summary: The key insights from our discussion are summarized below.
- For a diverging lens, the image is always virtual/upright/smaller.
- For a converging lens, the image can be virtual/upright/larger or real/inverted/(smaller or larger) depending on where the object is kept.
These results are tabulated below. Comparing with the analogous table for mirrors, we can see that a diverging lens has the exact same behavior as a convex mirror (both have negative focal length), and converging lenses behave similar to concave mirrors (both have positive focal length). This should come as no surprise, since the mirror equation is identical to the thin lens equation with the appropriate sign convention.
| Object location | Diverging Lens ( |
Converging Lens ( |
|---|---|---|
This behavior can also be marked on plots of the image vs. object distance as shown below.