Lensing by oil on water

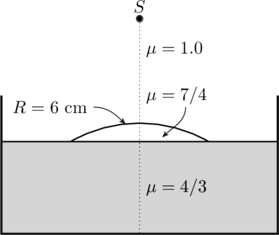
JEE Advanced 2011 Paper 2, Question 36

Water (with refractive index $=\frac{4}{3}$ ) in a tank is $18 \mathrm{~cm}$ deep. Oil of refractive index $\frac{7}{4}$ lies on water making a convex surface of radius of curvature $R=6 {\rm ~cm}$ as shown. Consider oil to act as a thin lens. An object ‘ $S$ ’ is placed $24 \mathrm{~cm}$ above water surface. The location of its image is at ‘ $x$ ’ cm above the bottom of the tank. What is ‘ $x$ ’?

Rendered by QuickLaTeX.com

Solution

To find the location of the final image we consider the oil and the water in the tank as a combination of two elements: a lens and a flat refracting surface. To calculate its focal length we use the Lens maker’s formula,

(1) $\begin{equation*} \frac{1}{f} = (n - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right) \end{equation*}$

where $n \equiv n_2/n_1$ is the ratio of refractive index $n_2$ of the material of the lens to that of the surrounding medium $n_1$ . The lens is made of oil, so $n_2 = \mu_{\rm oil}$ . But here is a problem: the oil lens has air on one side and water on the other, so what is $n_1$ ?

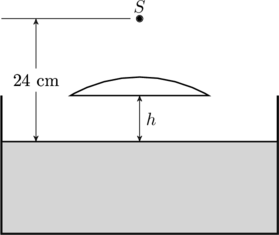
To resolve this issue we imagine the lens is actually floating in air above the surface of the water at some height $h$ (see figure). This allows us to take the refractive index of the medium surrounding the lens as $n_1=\mu_{\rm air}=1$ , and we can apply (1) without ambiguity. Once we locate the image formed due to this floating lens we can take $h \to 0$ and use that to find the position of the final image.

Noting that the lens has radii of curvature $R_1=6 {\rm ~cm}$ and $R_2=\infty$ (cf. this figure), its focal length is given by

(2) $\begin{equation*} \frac{1}{f} = (\mu_{\rm oil} - 1) \left( \frac{1}{R_1} - \frac{1}{R_2} \right) = \frac{3}{4} \times \frac{1}{6 {\rm~cm}} \implies f = +8 {\rm~cm} . \end{equation*}$

The object $S$ is at a distance $p=+(24-h) {\rm~cm}$ from this lens and it forms an intermediate image at $q$ ,

(3) $\begin{equation*} \frac{1}{q} = \frac{1}{f}-\frac{1}{p} = \frac{1}{+8 {\rm~cm}}-\frac{1}{+(24-h) {\rm~cm}} \implies q \overset{h \to 0}{=} + 12 {\rm~cm} . \end{equation*}$

In the last step we have taken $h \to 0$ , which returns us to the original problem. The positive sign of $q$ tells us that the image was formed under the lens at a depth of $12 {\rm~cm}$ from it (see sign convention for lenses). We can take this to be the position of the object for the refracting surface separating the water and air. The positions of the object and image for such a surface satisfy

(4) $\begin{equation*} \frac{\mu_{\rm air}}{s} + \frac{\mu_{\rm water}}{s'} = 0 \end{equation*}$

The first relation is obtained by taking the general formula for a refracting surface (see (27-3) of this Feynman lecture or the last equation on this page) and taking the radius of curvature to infinity. The distances $s$ and $s'$ follow the same sign convention as lenses. Now here is the important point: we located the intermediate image from the lens at $12 {\rm~cm}$ below the lens by assuming that the space below the lens had air. Since this is the object for the refracting surface we must take the object to be in air at a distance $s=-12 {\rm~cm}$ , even though, by the sign convention (see figure), this point is under water.

Rendered by QuickLaTeX.com — The sign convention for the refracting surface separating air and water. The air side is assumed to be the object side.

Then, (4) yields

(5) $\begin{equation*} s' = - \frac{\mu_{\rm water}}{\mu_{\rm air}} s = -\frac{4}{3} \times -12 {\rm~cm} = +16 {\rm~cm} . \end{equation*}$

Since the tank is $18 {\rm~cm}$ deep, $\boxed{x = 18 {\rm~cm} - 16 {\rm~cm} = 2 {\rm~cm}}$ .

Leave a Reply Cancel reply