A lens is a refracting element with two curved surfaces. Light changes direction as it refracts through each of these surfaces. If the thickness of the lens is small compared to the radius of curvature of each surface, we can think of light as bending just once at the central plane of the lens. This approximation is justified more rigorously in chapter 27 of the Feynman lectures. For our present discussion we start with equation (27.12) from that book, called the thin lens equation,
(1) ![]()
where ![]() is the object distance from the lens,
is the object distance from the lens, ![]() is the image distance, and
is the image distance, and ![]() is the focal length of the lens. The sign convention for these distances are given in the table. This convention is different from that of mirrors, given here.
is the focal length of the lens. The sign convention for these distances are given in the table. This convention is different from that of mirrors, given here.
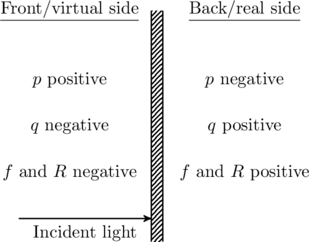
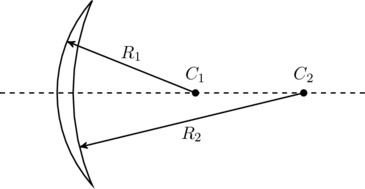
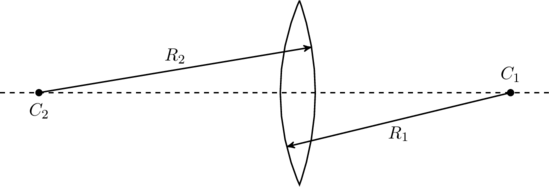
The symbol ![]() in this table refers to the radii of curvature of the two spherical surfaces of the lens. For example, consider the lens shown in figure. This is the shape of a contact lens prescribed by opthamologists. If we keep the object on the left side, light from the object falls on the first surface with a radius of curvature
in this table refers to the radii of curvature of the two spherical surfaces of the lens. For example, consider the lens shown in figure. This is the shape of a contact lens prescribed by opthamologists. If we keep the object on the left side, light from the object falls on the first surface with a radius of curvature ![]() , passes through the material of the lens, and refracts out through the second surface of radius
, passes through the material of the lens, and refracts out through the second surface of radius ![]() . These surfaces can be thought of as sections of two spheres with radii
. These surfaces can be thought of as sections of two spheres with radii ![]() and
and ![]() centered at points
centered at points ![]() and
and ![]() respectively. Since both radii are on the back side of the lens, they are positive by the table.
respectively. Since both radii are on the back side of the lens, they are positive by the table.
 and
and  .
.Similarly, we can have other lens shapes by moving around the centers of the two spherical surfaces. If we move ![]() to the front side, we get a biconvex lens, as shown in figure. The radius
to the front side, we get a biconvex lens, as shown in figure. The radius ![]() is still positive but
is still positive but ![]() is negative in this case, since that radius is in front of the lens.
is negative in this case, since that radius is in front of the lens.
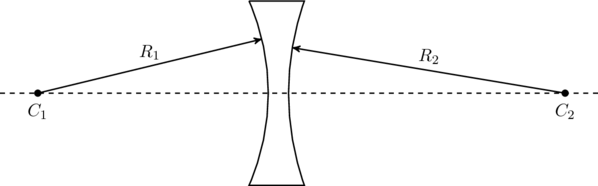
As a final example, consider the biconcave lens in figure. Here, the radius ![]() is negative and
is negative and ![]() is positive.
is positive.
 and
and  .
.The radii of curvature of the lens surfaces, and the index of refraction ![]() of the lens material determine the focal length of the lens through the Lens Maker’s formula,
of the lens material determine the focal length of the lens through the Lens Maker’s formula,
(2) ![]()
The signs of the radii are crucial in determining the value and sign of ![]() , which in turn relates the object and image distances through (1). For example, any biconvex lens (figure) is guaranteed to have a positive focal length since
, which in turn relates the object and image distances through (1). For example, any biconvex lens (figure) is guaranteed to have a positive focal length since
(3) ![]()
In the second step we write ![]() since it is negative. The resulting expression is a sum of two positive numbers,
since it is negative. The resulting expression is a sum of two positive numbers, ![]() and
and ![]() , multiplied by
, multiplied by ![]() which is also positive (since
which is also positive (since ![]() ). A positive
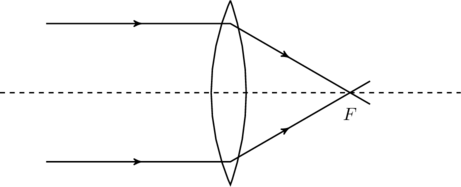
). A positive ![]() falls on the back side of the lens (see the table), which means that light rays coming from infinity in front of the lens are brought to focus at a point
falls on the back side of the lens (see the table), which means that light rays coming from infinity in front of the lens are brought to focus at a point ![]() behind the lens as shown in figure. A lens with positive focal length is called a converging lens.
behind the lens as shown in figure. A lens with positive focal length is called a converging lens.
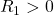 and
and 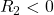 .
.We can also have diverging lenses, which have negative focal length. Any biconcave lens, like the one in figure, will have a negative focal length since
(4) ![]()
Apparently, light from infinity is brought to focus in front of this lens. In reality, the parallel light rays incident on the lens diverges after refraction through the lens, and the diverging rays can be extrapolated backwards to meet at a point ![]() in front of the lens as illustrated in figure. The image in this case is called virtual which means, to an observer behind the lens the diverging light rays appear to come from
in front of the lens as illustrated in figure. The image in this case is called virtual which means, to an observer behind the lens the diverging light rays appear to come from ![]() even though those rays never actually pass through
even though those rays never actually pass through ![]() . We will see more examples of virtual images in the next chapter.
. We will see more examples of virtual images in the next chapter.
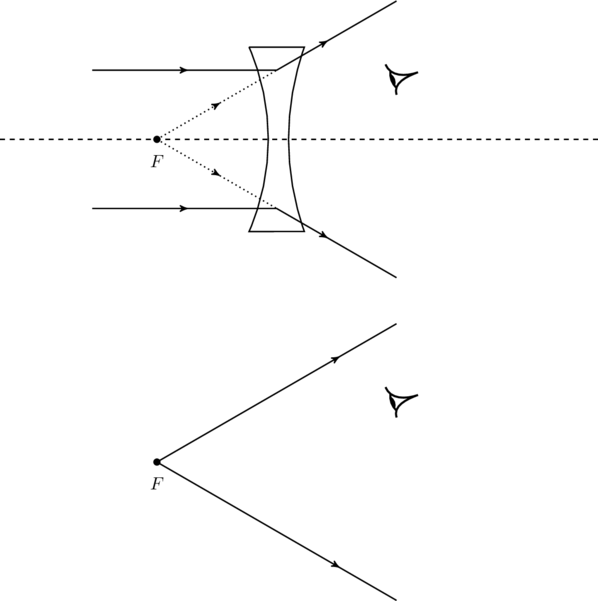
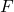 (top figure). That means an observer exposed to the diverging rays behind the lens gets the impression that those rays are coming from
(top figure). That means an observer exposed to the diverging rays behind the lens gets the impression that those rays are coming from 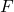 (bottom figure) when in fact they never passed through
(bottom figure) when in fact they never passed through 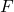 . Such images are called virtual.
. Such images are called virtual.Lenses have two focal points (or foci) because we can keep the object on either side of the lens (unlike a mirror). We will denote one of these by ![]() and the other by
and the other by ![]() (see for example figure and figure).
(see for example figure and figure). ![]() is the point at which light from infinity coming from the front is brought to focus. Light leaving object kept at
is the point at which light from infinity coming from the front is brought to focus. Light leaving object kept at ![]() will form an image at infinity behind the lens. For a thin lens both focal points are the same distance
will form an image at infinity behind the lens. For a thin lens both focal points are the same distance ![]() from the lens. That is, thin lenses have two focal points but only one focal length. The distinction between
from the lens. That is, thin lenses have two focal points but only one focal length. The distinction between ![]() and
and ![]() is important for ray tracing.
is important for ray tracing.
Exercise: If the five lenses shown below are made of the same material which lens has the shortest positive focal length?
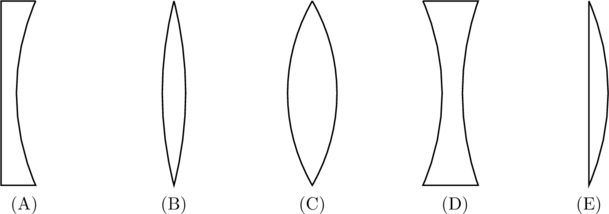
Solution: The focal length of a lens is given by
(5) ![]()
If we keep the object on the left, the radii will be positive on the right side of the lens. ![]() is the radius of the first surface the incident light hits, and
is the radius of the first surface the incident light hits, and ![]() is the radius of the second surface. We can use this to determine the sign of the focal length for each lens,
is the radius of the second surface. We can use this to determine the sign of the focal length for each lens,
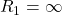 and
and 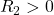 , which means
, which means 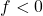 ,
,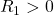 and
and 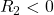 , which means
, which means 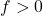 ,
,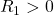 and
and 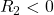 , which means
, which means 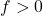 ,
, and
and 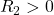 , which means
, which means 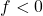 ,
,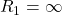 and
and 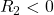 , which means
, which means 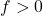 .
.
(A) and (D) have negative focal length (i.e.\ they are diverging lenses), so they can’t be the answer. Of the possible options, the thicker lens (C) has the smallest radii. If we compare (B) and (C),
(6) ![]()
since ![]() etc. Similarly we can also compare (C) and (E) to see the
etc. Similarly we can also compare (C) and (E) to see the ![]() as well. Therefore, (C) has the shortest focal length.
as well. Therefore, (C) has the shortest focal length.
We could also have come to the conclusion using a physical argument. Consider a lens with infinitely large ![]() and
and ![]() . This is essentially a thin slab of glass. Light from infinity will not be brought to focus after passing through this `lens’, which means it has a focal length of
. This is essentially a thin slab of glass. Light from infinity will not be brought to focus after passing through this `lens’, which means it has a focal length of ![]() . If we now introduce a small curvature to either surface of the lens, light rays will be bent toward the optical axis. Since infinite radii of curvature gave us an infinite radius of curvature, the lens with the shortest focal length should be the one with the shortest radii. This is option (C).
. If we now introduce a small curvature to either surface of the lens, light rays will be bent toward the optical axis. Since infinite radii of curvature gave us an infinite radius of curvature, the lens with the shortest focal length should be the one with the shortest radii. This is option (C).