Question 1
A string of length ![]() is clamped at each end and vibrates in a standing wave pattern. The wavelengths of the constituent traveling waves cannot be:
is clamped at each end and vibrates in a standing wave pattern. The wavelengths of the constituent traveling waves cannot be:
Question 2
If the speed of sound is 340 m/s, the length of the shortest open-closed pipe that resonates at 218 Hz is:
- 23 cm
- 17 cm
- 39 cm
- 78 cm
- 1.6 cm
Question 3
At ![]() , a pipe open at both ends resonates at a frequency of 440 Hz. At what frequency does the same pipe resonate on a particularly cold day when the speed of sound is 3 percent lower than it would be at
, a pipe open at both ends resonates at a frequency of 440 Hz. At what frequency does the same pipe resonate on a particularly cold day when the speed of sound is 3 percent lower than it would be at ![]() ?
?
- 433 Hz
- 427 Hz
- 453 Hz
- 440 Hz
- 414 Hz
Question 4
A tuning fork is sounded above a resonating tube (one end closed), which resonates at a length of 0.2 m and again upon extension at 0.6 m. If the tube length were extended even further, at what point will the sound from the tuning fork again resonate in the tube?
- 0.8 m
- 1.0 m
- 1.2 m
- 1.6 m
- 2.0 m
Question 5
A standing wave is set up in a 2.0 m string fixed at both ends. The string vibrates in 5 distinct segments when driven by a 120 Hz source. In how many of the segments will the string vibrate if the tension is increased by a factor of 4?
Hint: For a string,
(1) 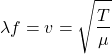
where ![]() is the string tension and
is the string tension and ![]() is the mass per unit length.
is the mass per unit length.
- 3
- 10
- 20
- 30
- No standing wave pattern will be observed
Question 6
Two strings made of different materials are joined together and stretched between rigid walls as shown in the figure. The strings are of equal length and have mass per unit length of ![]() g/m and
g/m and ![]() g/m. Standing waves are setup in this arrangement with the joint as one of the nodes. What is the ratio of the wavelengths
g/m. Standing waves are setup in this arrangement with the joint as one of the nodes. What is the ratio of the wavelengths ![]() in these two strings?
in these two strings?

- 1/4
- 1/2
- 1
- 2
- 4
Question 7
When two tuning forks (A and B) are sounded at the same time, you also observe a beat frequency of 6 Hz if B has a frequency of 245 Hz and a beat frequency of 3 Hz if B has a frequency of 248 Hz. What is the frequency of A?
- 239 Hz
- 248 Hz
- 251 HZ
- 254 HZ
- More than one frequency could be correct.
Solutions
Question 1: (E). The standing wave on the string will have an integer number of nodes, separated by a distance ![]() . That is, the length of the string must be
. That is, the length of the string must be ![]() . From this relation we see that
. From this relation we see that ![]() which is satisfied by all options except
which is satisfied by all options except ![]() .
.
Question 2: (C). The wavelength of the sound wave will be ![]() . The shortest open-closed pipe that resonates will have a length
. The shortest open-closed pipe that resonates will have a length ![]() cm.
cm.
Question 3: (B). Since the length of the pipe is fixed the wavelength of the harmonics don’t change. That means the frequency ![]() reduces in proportion to the velocity
reduces in proportion to the velocity ![]() . Thus
. Thus ![]() Hz.
Hz.
Question 4: (B). Since the frequency of the tuning fork is fixed wavelength of the wave is the same in all cases (recall ![]() ). That means we get resonance everytime the tube extends by half a wavelength starting from the first harmonic at 0.2 m. So
). That means we get resonance everytime the tube extends by half a wavelength starting from the first harmonic at 0.2 m. So ![]() m, and after 0.6 m the next resonance will be when the tube length is
m, and after 0.6 m the next resonance will be when the tube length is ![]() m.
m.
Question 5: (E). Each of the distinct segments is half a wavelength. That means ![]() m or
m or ![]() m. Then, with
m. Then, with ![]() Hz we get
Hz we get ![]() m/s. If
m/s. If ![]() , then
, then ![]() since
since ![]() also. With
also. With ![]() kept fixed at 120 Hz, this means
kept fixed at 120 Hz, this means ![]() m. But we can’t divide a 2 m string into an integer number segments of
m. But we can’t divide a 2 m string into an integer number segments of ![]() m each, which means no standing wave pattern is possible.
m each, which means no standing wave pattern is possible.
Question 6: (D). The tension ![]() in both strings are the same, which means the wave velocities in the strings are related as
in both strings are the same, which means the wave velocities in the strings are related as
(2) ![]()
Furthermore the frequency of a wave does not change from one medium to the next, which means
(3) ![]()
Question 7: (C). The beat frequency is ![]() , which means
, which means ![]() . With the given information we see that
. With the given information we see that ![]() Hz, and
Hz, and ![]() Hz. The only option that fits both experiments is
Hz. The only option that fits both experiments is ![]() Hz.
Hz.