The usual discussions of geometrical optics often rely too heavily on ray diagrams to locate the image and study its properties. We will demonstrate that all of these insights can be obtained purely by algebra on the mirror equation. Developing these instincts will help us solve optics problems without having to use crude, hand drawn, and often inaccurate ray diagrams. Our main results are summarized in the table below.
We begin by recalling the mirror equation
(1) ![]()
where ![]() and
and ![]() the distances of the object and image from the mirror, and the focal length
the distances of the object and image from the mirror, and the focal length ![]() , for a spherical mirror with radius of curvature
, for a spherical mirror with radius of curvature ![]() . The magnification is given by
. The magnification is given by
(2) ![]()
If ![]() is positive, it means the image is upright (for an upright object). Otherwise it is inverted. The size of the image is
is positive, it means the image is upright (for an upright object). Otherwise it is inverted. The size of the image is ![]() . In applying the above formulas we need to be careful about the signs of
. In applying the above formulas we need to be careful about the signs of ![]() ,
, ![]() , and
, and ![]() or
or ![]() . The convention is summarized below. The front side of the mirror is the region where light originates and moves toward the mirror.
. The convention is summarized below. The front side of the mirror is the region where light originates and moves toward the mirror.
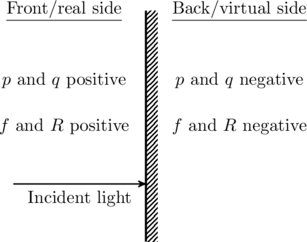
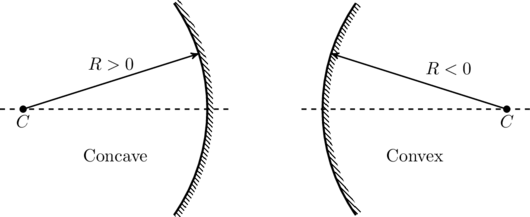
Based on this convention, concave mirrors have positive radius of curvature ![]() and focal length
and focal length ![]() , whereas convex mirrors have negative values for these parameters (see figure).
, whereas convex mirrors have negative values for these parameters (see figure).
Plane Mirrors
We know from experience that a plane mirror produces an image of the same size as the object, and the image appears as far behind the mirror as the object is in front of it. In fact, taking ![]() in (1) leads to the relation
in (1) leads to the relation ![]() . That is, a plane mirror can be thought of as a spherical mirror of infinite radius of curvature, and consequentially, infinite focal length. Furthermore, the magnification is
. That is, a plane mirror can be thought of as a spherical mirror of infinite radius of curvature, and consequentially, infinite focal length. Furthermore, the magnification is ![]() which means the image is upright and has the same size as the object.
which means the image is upright and has the same size as the object.
Convex Mirrors
The focal length of a convex mirror is negative, so we may write it as ![]() in (1),
in (1),
(3) ![]()
This equation can tell us everything we want to know about the location and size of the image for various positions of the object.
![]()
To start with, notice that if we keep the object at infinity (that is, the incident rays are all parallel to the optical axis) then ![]() , which makes
, which makes ![]() . Furthermore, the magnification is zero since
. Furthermore, the magnification is zero since ![]() . Therefore the image will be at the focal point, which is on the back side of the convex mirror (see figure). Since no light can actually reach this side we infer that the image is virtual, that is, the image is a point from which the reflected light appears to emanate.
. Therefore the image will be at the focal point, which is on the back side of the convex mirror (see figure). Since no light can actually reach this side we infer that the image is virtual, that is, the image is a point from which the reflected light appears to emanate.
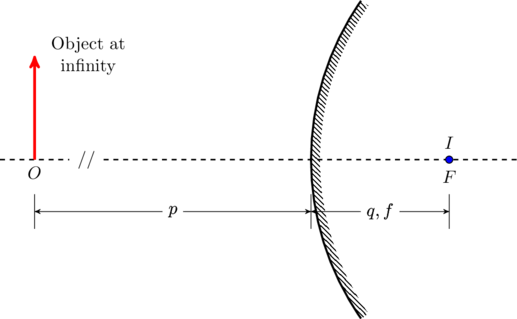
![]()
Next, we consider a finite, positive ![]() . Then, (3) yields
. Then, (3) yields
(4) ![]()
It is apparent that ![]() will be negative for all positive
will be negative for all positive ![]() — the image will always be formed behind the convex mirror for an object kept in its front. Also, the r.h.s. of this equation is lesser than
— the image will always be formed behind the convex mirror for an object kept in its front. Also, the r.h.s. of this equation is lesser than ![]() , and therefore
, and therefore
(5) ![]()
where, in the last step, we’ve used that fact that ![]() is negative. A negative
is negative. A negative ![]() also ensures that the magnification
also ensures that the magnification ![]() will always be positive. We can constrain
will always be positive. We can constrain ![]() further by taking
further by taking ![]() where
where ![]() . Then (4) gives
. Then (4) gives
(6) ![]()
But that implies
(7) ![]()
since ![]() . Thus the image will always be smaller than the object, with farther objects shrunk down to a greater extend. We conclude that, for any
. Thus the image will always be smaller than the object, with farther objects shrunk down to a greater extend. We conclude that, for any ![]() , the image is upright, smaller, and located somewhere between the mirror surface and its focal point
, the image is upright, smaller, and located somewhere between the mirror surface and its focal point ![]() (see figure). The first two features allow a convex mirror to have a larger field of view than a regular plane mirror. This is why rear/side view mirrors in cars are convex (cf. this).
(see figure). The first two features allow a convex mirror to have a larger field of view than a regular plane mirror. This is why rear/side view mirrors in cars are convex (cf. this).
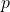
Concave Mirrors
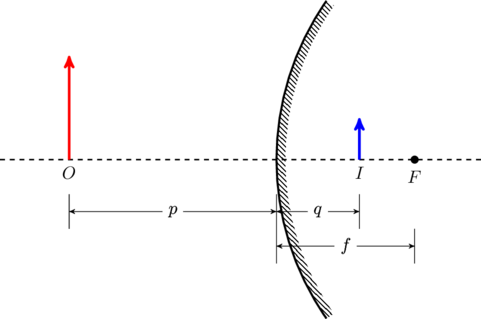
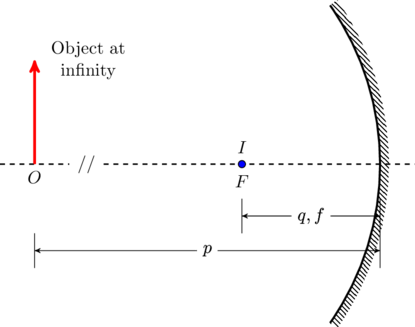
Concave mirrors have positive focal length, resulting in a dramatically different behavior compared to what we saw in the convex case. Once again, we will consider each situation carefully.
![]()
Taking ![]() in (1) we find that
in (1) we find that ![]() , which is positive. So a parallel beam of light is brought to focus at the focal point
, which is positive. So a parallel beam of light is brought to focus at the focal point ![]() in front of the mirror (see figure). This is a real image because we can capture this light on a small screen kept at
in front of the mirror (see figure). This is a real image because we can capture this light on a small screen kept at ![]() .
.
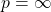
![]()
If the object is kept a finite distance ![]() , then
, then
(8) ![]()
Therefore ![]() is still positive; the image is formed in front of the lens, and it is real. Furthermore,
is still positive; the image is formed in front of the lens, and it is real. Furthermore,
(9) ![]()
which means the object is farther from the mirror than the focal point ![]() . Since
. Since ![]() and
and ![]() are both positive, the magnification
are both positive, the magnification ![]() is negative (cf. (2)), which means the image will be inverted. Whether the image is enlarged (
is negative (cf. (2)), which means the image will be inverted. Whether the image is enlarged (![]() ) or shrunk (
) or shrunk (![]() ) depends on the value of
) depends on the value of ![]() . For
. For ![]() ,
,
(10) ![]()
Consequently, ![]() and the image is smaller compared to the object (see figure).
and the image is smaller compared to the object (see figure).
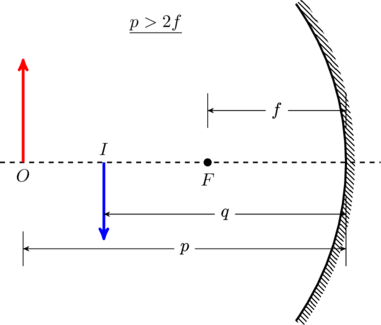
Conversely, if ![]() we find
we find ![]() (this is an example of reciprocity). In that case,
(this is an example of reciprocity). In that case, ![]() and the image is enlarged.
and the image is enlarged.
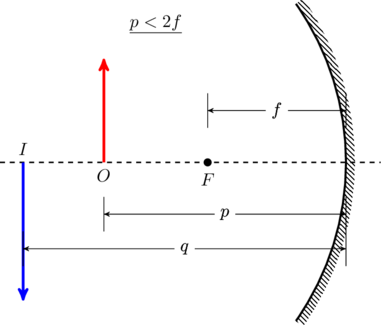
![]()
If the object is brought closer to the mirror than its focal length, we have ![]() , as a result of which
, as a result of which
(11) ![]()
Therefore, ![]() is negative and the image is formed behind the lens; it is virtual. Also,
is negative and the image is formed behind the lens; it is virtual. Also,
(12) ![]()
which means ![]() ; the image is enlarged (see figure).
; the image is enlarged (see figure).

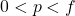
Notice that as the object passes through ![]() there is an abrupt transition in position and nature of the image. If we keep the object slightly to the left of
there is an abrupt transition in position and nature of the image. If we keep the object slightly to the left of ![]() , at
, at ![]() , the image is formed at
, the image is formed at ![]() with
with ![]() . Placing the object slightly to the right of
. Placing the object slightly to the right of ![]() , at
, at ![]() produces an image at
produces an image at ![]() with
with ![]() . It is as if the image travelled to
. It is as if the image travelled to ![]() in the left direction, passed through it, and ended up on the right/back side as the object moved from
in the left direction, passed through it, and ended up on the right/back side as the object moved from ![]() to
to ![]() . It is a common theme in nature that such jarring changes in physical behavior are associated with some number going through infinity.
. It is a common theme in nature that such jarring changes in physical behavior are associated with some number going through infinity.
Summary
The mirror equation (1) gives a surprising amount of information about the position, magnification and nature (real/virtual) of the image if we apply the conventions carefully. The results are summarized in the table below. Of course, if the exact values of ![]() and
and ![]() are specified, little to no creativity is required compute the image location.
are specified, little to no creativity is required compute the image location.
| Object location | Convex ( |
Concave ( |
|---|---|---|