Triangle on a concave mirror

JEE Advanced 2018 Paper 2, Question 4

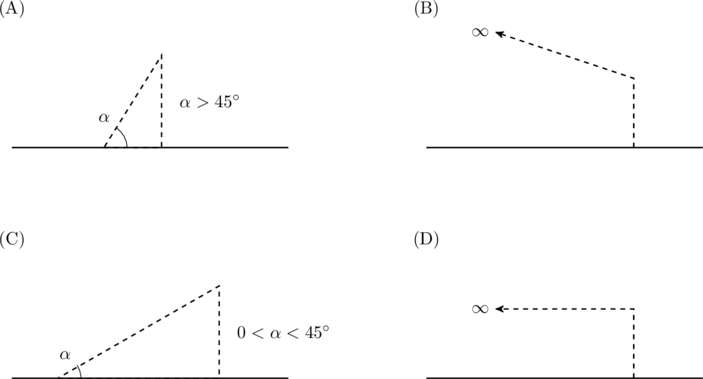
A wire is bent in the shape of a right angled triangle and is placed in front of a concave mirror of focal length $f$ , as shown in the figure. Which of the figures shown in the four options qualitatively represent(s) the shape of the image of the bent wire? (These figures are not to scale.)

Rendered by QuickLaTeX.com

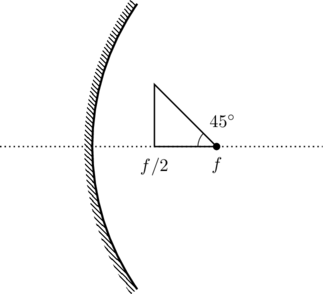
Related article: Optics without ray diagrams: Mirrors

Solution

If the object is kept between a concave mirror and its focal point the image is virtual and upright (see this note). Recall that an object at a distance $p$ from a mirror of focal length $f$ forms an image at $q$ , such that

(1) $\begin{equation*} \frac{1}{p} + \frac{1}{q} = \frac{1}{f} . \end{equation*}$

The given object is extensive, that is, different points of the object are located at different $p$ . The point $B$ is at $p=f$ (see figure), which means there will be a portion of the image at $q = -\infty$ . Therefore, the correct option must be either (B) or (D). To narrow it down further let us consider the segment $AB$ . The point $A$ is $(h_0,f/2)$ and $B$ is $(0,f)$ (the triangle is isoceles, which means $h_0=f/2$ , but we will continue calling this height $h_0$ for the time being). An arbitrary point on the segment $AB$ is given by

(2) $\begin{equation*} \frac{h-y_B}{p-x_B} = \frac{y_A-y_B}{x_A-x_B} \implies h = \frac{2 h_0}{f} (f-p) . \end{equation*}$

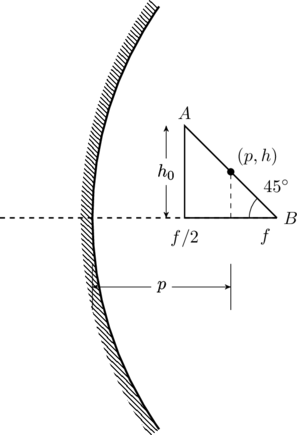
This point will be located at a distance $q$ given by (1),

(3) $\begin{equation*} q = \frac{f p}{p-f} , \end{equation*}$

with a height $h' = M \times h$ , where $M = -q/p$ is the magnification. That is,

(4) $\begin{equation*} h' = \frac{-\frac{f p}{p-f}}{p} \times \frac{2 h_0}{f} (f-p) = 2 h_0 , \end{equation*}$

which is a constant. Therefore all points on $AB$ appear at the same height in the image. Therefore, the correct answer is (D).

Discussion: The points on the pricipal axis between $f/2$ and $f$ will also be be in the image, although this is not clear from the picture given in the exam. A better illustration would be the figure below.

Rendered by QuickLaTeX.com

Also note that $h' = 2 h_0$ for any height $h_0$ (within the field of view of the mirror, of course). That is, the image has the shape shown above for any $\angle B$ , and not just $\angle B = 45^\circ$ .

Leave a Reply Cancel reply