JEE Advanced 2017 Paper 1, Question 2
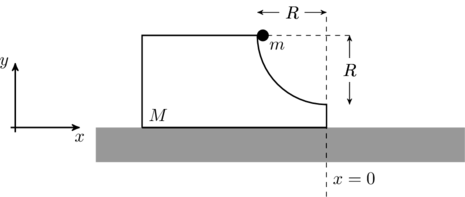
A block of mass ![]() has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at
has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at ![]() , in a co-ordinate system fixed to the table. A point mass
, in a co-ordinate system fixed to the table. A point mass ![]() is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is
is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is ![]() and the velocity is
and the velocity is ![]() . At that instant, which of the following options is/are correct?
. At that instant, which of the following options is/are correct?
- The position of the point mass
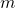 is:
is: 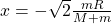
- The velocity of the point mass
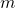 is:
is: 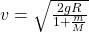
- The
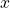 component of displacement of the center of mass of the block
component of displacement of the center of mass of the block 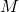 is:
is: 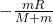
- The velocity of the block
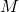 is:
is: 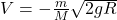
Related problem: Mass on a semicircular block.
Solution
Suppose the mass ![]() has a velocity
has a velocity ![]() , and the block has a velocity
, and the block has a velocity ![]() at the instant
at the instant ![]() loses contact with the block, as shown in the figure below.
loses contact with the block, as shown in the figure below.

Since the surfaces are frictionless, energy is conserved. Furthermore there is no external force in the ![]() direction, which means momentum is conserved along the horizontal axis. Then,
direction, which means momentum is conserved along the horizontal axis. Then,
(1) 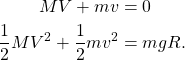
In writing these equations we have used the fact that the initial momentum of the system is zero, and the total potential energy decreases by ![]() . Denoting the final momentum of the mass
. Denoting the final momentum of the mass ![]() as
as ![]() , we may write the energy conservation equation gives
, we may write the energy conservation equation gives
(2) 
We have chosen the positive square root because the mass ![]() ends up moving in the
ends up moving in the ![]() direction. Thus,
direction. Thus,
(3) 
Calculating the diplacement of the masses is slightly more involved because we need to integrate the velocity at each instant of time from start to finish. Furthermore, when the mass ![]() is rolling down the circular cut there are two parts to its motion: the circular motion as it rolls down the cut, and the horizontal displacement as it remains in contact with the moving block during transit. In such situations the fool proof method to find the correct velocity is the write down the position of the mass in question and take its time derivative.
is rolling down the circular cut there are two parts to its motion: the circular motion as it rolls down the cut, and the horizontal displacement as it remains in contact with the moving block during transit. In such situations the fool proof method to find the correct velocity is the write down the position of the mass in question and take its time derivative.
Tip: To find the velocity of a mass undergoing “compound” motion, write down an expression for its position and differentiate it with respect to time.
Here is how it works. We choose a co-ordinate system as shown in figure. The top right corner of the block is ![]() , and the mass
, and the mass ![]() makes an angle
makes an angle ![]() with respect to the horizontal, as indicated.
with respect to the horizontal, as indicated.
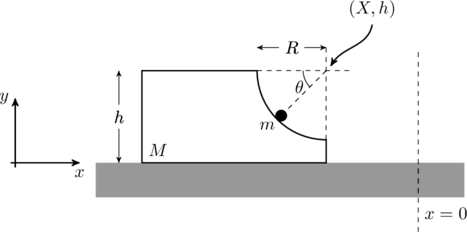
The mass ![]() is at a position
is at a position
(4) ![]()
The velocity of ![]() is
is
(5) ![]()
where the overhead dots represent derivatives w.r.t. time, ![]() . The velocity of the block is
. The velocity of the block is ![]() . Again, by conservation of momentum in the horizontal direction
. Again, by conservation of momentum in the horizontal direction
(6) ![]()
which we can invert to obtain
(7) ![]()
At the moment it loses contact with the block, the total horizontal displacement of the mass ![]() is the same as the
is the same as the ![]() co-ordinate of the corner,
co-ordinate of the corner,
(8) ![]()
(9) ![]()
This ![]() is also the displacement of the center of mass of the block. Thus, we conclude that option (A) is incorrect but option (C) is correct.
is also the displacement of the center of mass of the block. Thus, we conclude that option (A) is incorrect but option (C) is correct.