A heavy particle of mass ![]() is placed at the top of a semicircular block of radius
is placed at the top of a semicircular block of radius ![]() . Find the height at which the particle falls off, assuming (i) the block is fixed to the ground, and (ii) the block has a mass
. Find the height at which the particle falls off, assuming (i) the block is fixed to the ground, and (ii) the block has a mass ![]() and is free to move. Assume all surfaces are frictionless.
and is free to move. Assume all surfaces are frictionless.

Related problem: Sliding on a block with a circular cut.
Solution:
(i) We first consider the case where the block is fixed to the ground. As the mass slides down the block, there are three forces acting on it: the weight ![]() , the centrifugal force
, the centrifugal force ![]() , and the normal reaction force from the block.
, and the normal reaction force from the block.
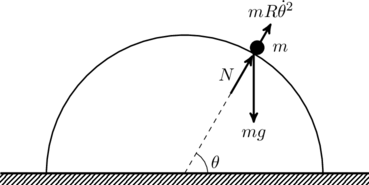
When the mass is sliding on the semicircular block, there is no motion in the radial direction, which means the net radial force is zero,
(1) ![]()
At the instant the particle loses contact with the block the normal force ![]() will be zero. To find the angle
will be zero. To find the angle ![]() at which this happens we need to find an expression for the angular velocity
at which this happens we need to find an expression for the angular velocity ![]() in terms of
in terms of ![]() . We can accomplish this by noting that the total energy of the system is the sum of the kinetic and potential energies of the mass
. We can accomplish this by noting that the total energy of the system is the sum of the kinetic and potential energies of the mass ![]() ,
,
(2) ![]()
The initial energy is ![]() , when the particle is at the very top of the block. In the absence of friction, energy is conserved, and we may write
, when the particle is at the very top of the block. In the absence of friction, energy is conserved, and we may write
(3) ![]()
Inverting this equation, we obtain
(4) ![]()
which can be plugged into (1) (with ![]() ) to find
) to find ![]() . Thus, the mass
. Thus, the mass ![]() falls off at a height
falls off at a height
(5) ![]()
(ii) The problem becomes much more interesting when the block is allowed to slide. The central idea is the same as above: we want to find the angle at which ![]() becomes zero. However, the block is accelerating with the mass
becomes zero. However, the block is accelerating with the mass ![]() still in contact, so there is an additional fictitious force on
still in contact, so there is an additional fictitious force on ![]() .
.
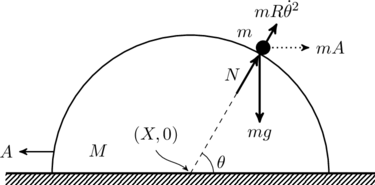
If we denote the horizontal acceleration of the block as ![]() , then the fictitious force on
, then the fictitious force on ![]() is
is ![]() , as indicated above. The net radial force on the
, as indicated above. The net radial force on the ![]() must still be zero so long as it is touching the semicircle,
must still be zero so long as it is touching the semicircle,
(6) ![]()
As mentioned above, ![]() becomes zero at the instant the mass loses contact with the block. In addition, the acceleration
becomes zero at the instant the mass loses contact with the block. In addition, the acceleration ![]() also becomes zero at exactly this instant — with the mass
also becomes zero at exactly this instant — with the mass ![]() no longer exerting its weight on the block the latter stops accelerating. Therefore, we want to find the angle
no longer exerting its weight on the block the latter stops accelerating. Therefore, we want to find the angle ![]() such that
such that
(7) ![]()
which is exactly the condition we had in part (i). However, the expression for ![]() will be more involved. While
will be more involved. While ![]() remains in contact with the block, its motion involves linear motion due to displacement of the block and circular motion as it slides down the semicircle. To find the velocity of
remains in contact with the block, its motion involves linear motion due to displacement of the block and circular motion as it slides down the semicircle. To find the velocity of ![]() it is easiest to find its position and differentiate it with respect to time. If the center of the semicircle is at
it is easiest to find its position and differentiate it with respect to time. If the center of the semicircle is at ![]() at some instant (see figure), then
at some instant (see figure), then ![]() is located at
is located at
(8) ![]()
The velocity ![]() is
is
(9) ![]()
and its magnitude squared is
(10) ![]()
The total energy is the sum of kinetic energies of ![]() and
and ![]() , and the potential energy of
, and the potential energy of ![]() ,
,
(11) 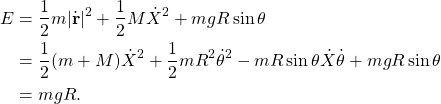
In the last step we have used conservation of energy to set ![]() . To express
. To express ![]() in terms of
in terms of ![]() , we need to eliminate
, we need to eliminate ![]() from the above equation. We do this by noting that momentum along the horizontal direction is conserved, since there is external force in that direction. Thus,
from the above equation. We do this by noting that momentum along the horizontal direction is conserved, since there is external force in that direction. Thus,
(12) ![]()
Substituting this in (11) we get
(13) 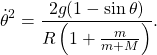
If we take ![]() this expression reduces to (4), as it should; when the mass of the block is much larger than
this expression reduces to (4), as it should; when the mass of the block is much larger than ![]() it barely moves and we return to the scenario is part (i). Plugging (13) this into (7), we find
it barely moves and we return to the scenario is part (i). Plugging (13) this into (7), we find
(14) ![]()
which has roots
(15) ![]()
We keep the positive root because ![]() . Thus, the mass
. Thus, the mass ![]() falls off the block at a height
falls off the block at a height
(16) 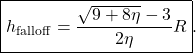
Bonus problem: Find the displacement of the block at the instant ![]() falls off.
falls off.