Missing energy in a rope and a capacitor

Consider a uniform rope of mass density $\lambda$ coiled on a smooth horizontal table. One end is pulled straight up with a constant speed $v_0$ as shown.

Find the force exerted on the end of the rope as function of the height $y$ .
Compare the power delivered to the rope with the rate of change of the rope’s mechanical energy.

(This is a problem from chapter 5 of Kleppner and Kolenkow)

Rendered by QuickLaTeX.com

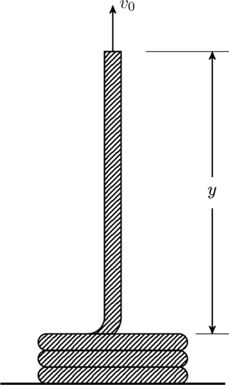
To find the force exerted at the top end, note that if we were to pull up a fixed mass with constant velocity $v_0$ , the total force on the mass should be zero since there is no change in momentum (Newton’s first law). In the present case, the net force will be non-zero because more of the rope is being pulled up over time so the mass is changing. If we denote the pulling force by $F$ and the momentum of the rope by $p$ , the net force is

(1) $\begin{equation*} F - \lambda y g = \frac{{\rm d} p}{{\rm d} t} . \end{equation*}$

Assuming the rope is inextensible, in a small time ${\rm d} t$ an extra segment of mass ${\rm d} m = \lambda v_0 {\rm d} t$ is pulled up with the rest of the rope, at velocity $v_0$ . The change in momentum in this time is

(2) $\begin{equation*} {\rm d} p = {\rm d} m \times v_0 = (\lambda v_0 {\rm d} t) v_0 . \end{equation*}$

Combining the above equations, we find

(3) $\begin{equation*} F = \lambda (y g + v_0^2) . \end{equation*}$

Next, the power delivered to the rope is just force $\times$ velocity,

(4) $\begin{equation*} P = F v_0 = \lambda v_0 (y g + v_0^2) . \end{equation*}$

The rate of change of energy of the rope can be calculated by once again considering the events in a time ${\rm d} t$ . First, the rope is raised by a height ${\rm d} y \equiv v_0 {\rm d} t$ . This is equivalent to adding a segment of length ${\rm d} y$ at the top end of the rope. Therefore, the potential energy of the rope changes by

(5) $\begin{equation*} {\rm d} U = (\lambda {\rm d} y) y g = \lambda y g v_0 {\rm d} t . \end{equation*}$

Next, the segment added at the end of the rope will add a kinetic energy

(6) $\begin{equation*} {\rm d} K = \frac{1}{2} (\lambda v_0 {\rm d} t) v_0^2 . \end{equation*}$

The differential change in energy is ${\rm d} E = {\rm d} K + {\rm d} U$ , and therefore the rate of change of energy is

(7) $\begin{equation*} \frac{{\rm d} E}{{\rm d} t} = \lambda v_0 \left( y g + \frac{1}{2} v_0^2 \right) . \end{equation*}$

We see a discrepancy between the power delivered to the rope and the rate of change of its energy. Why did this happen?

First, note that in writing (2) we assumed that the segment of mass ${\rm d} m$ goes from rest to $v_0$ instantaneously (the dashed curve in figure). In reality ${\rm d} m$ is initially at rest, and needs to be accelerated to velocity $v_0$ in time ${\rm d} t$ .
If we assume that this acceleration is uniform, the change in velocity of ${\rm d} m$ follows the solid black line in figure. Since the distance covered by ${\rm d} m$ is the area under this curve, we find that only $v_0 {\rm d} t/2$ additional length of the rope is pulled up in time ${\rm d} t$ . But if the rope is inextensible it can can only move up by the same distance as the length of the segment added at the bottom, which means the velocty of the rope is $v_0/2$ , not $v_0$ . This is the contradiction which leads to the difference between (4) and (7).

A similar situation occurs in the charging of a capacitor under incorrect idealizations. Consider a capacitor connected to a battery as shown in figure. We will assume that the wires are perfect conductors and the battery has no internal resistance.

When the switch $S$ is closed, the capacitor starts charging. Suppose the potential difference across the capacitor is $V \equiv Q/C$ at some instant of time. The work done in moving a small charge $+{\rm d} Q$ from the negative plate of the capacitor to the positive plate is ${\rm d} W = V {\rm d} Q$ . Charging ends when a charge $V_0 C$ has been transferred from one plate to the other this way. The total work done in charging up the capacitor is then

(8) $\begin{equation*} W = \int V {\rm d} Q = \frac{1}{C} \int_0^{V_0 C} Q {\rm d} Q = \frac{1}{2} V_0^2 C. \end{equation*}$

The work done by the battery in displacing this charge is simply

(9) $\begin{equation*} W_{\rm bat} = V_0 \times V_0 C = V_0^2 C . \end{equation*}$

It seems only half the work expended by the battery actually gets stored as energy in the capacitor. Where did the other half go? Since there are no resistances in the setup there is nothing to dissipate the energy. What gives?

To understand what happened recall the potential at every point on a perfect conductor must be the same. If we make the wires perfect conductors the potential difference across the battery and the capacitor must be equal at all times. Instead of the capacitor gradually building up potential as described above, we end up with an instantaneous transfer of charge which is unphysical. This is analogous to the infinite acceleration of the end of the rope as shown by the dashed line in figure.

We can fix the issue by introducing some resistance into the wires (see figure). If the switch is closed at $t=0$ , by Kirchoff’s Voltage Law we have

(10) $\begin{equation*} \frac{Q}{C} + R \frac{{\rm d} Q}{{\rm d} t} = V_0 , \quad t>0 . \end{equation*}$

The solution to this differential equation is

(11) $\begin{equation*} Q(t) = V_0 C (1 - e^{-t/RC}) . \end{equation*}$

For $t \ll RC$ , the charge on the capacitor approaches $V_0 C$ as expected. The current flowing through the resistance at any instant is $I(t) = {\rm d} Q/{\rm d} t = \frac{V_0}{R} e^{-t/RC}$ . Therefore, the total power dissipated in the resistance is

(12) $\begin{equation*} \int_0^\infty I^2(t) R \, {\rm d} t = \frac{V_0^2}{R} \int_0^\infty e^{-2 t/RC} {\rm d} t =\frac{1}{2} V_0^2 C . \end{equation*}$

This is exactly the missing energy we were looking for. The difference in energy spent by the battery and the energy stored in the capcitor is actually lost in the wires. Notice that the energy dissipated for any is independent of the value of the resistance; the only condition is that $R \neq 0$ . If the wires have a larger resistance the capacitor charges slower, which means the current through the wire is smaller. Thus, the energy lost in the wires is the same even though the capacitor takes longer to charge.

Leave a Reply Cancel reply