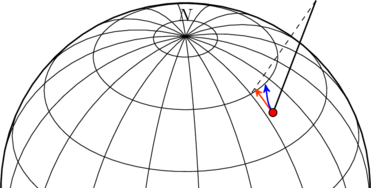
Imagine a mass ![]() moving on the surface of a rotating sphere. For instance, the mass could be parcel of air moving away from a high pressure region in the Earth’s atmosphere. It experiences a Coriolis force which, in the example shown in the figure below, pushes it from its original trajectory (orange) to move eastward (blue). Why does this happen, and how do we understand it intuitively?
moving on the surface of a rotating sphere. For instance, the mass could be parcel of air moving away from a high pressure region in the Earth’s atmosphere. It experiences a Coriolis force which, in the example shown in the figure below, pushes it from its original trajectory (orange) to move eastward (blue). Why does this happen, and how do we understand it intuitively?
Formally, the Coriolis force on ![]() is given by
is given by
(1) ![]()
where ![]() is the angular velocity of the rotating frame (Earth), and
is the angular velocity of the rotating frame (Earth), and ![]() is the velocity of
is the velocity of ![]() as seen by an observer on the Earth’s surface. This formula is derived in chapter 9 of Kleppner and Kolenkow, or here. We will now see how (1) can be understood as a consequence of the conservation of angular momentum.
as seen by an observer on the Earth’s surface. This formula is derived in chapter 9 of Kleppner and Kolenkow, or here. We will now see how (1) can be understood as a consequence of the conservation of angular momentum.
For simplicity, we first consider the situation shown in the figure. Two people ![]() and
and ![]() are standing on a large merry-go-round which is spinning with angular velocity
are standing on a large merry-go-round which is spinning with angular velocity ![]() . Person
. Person ![]() holds in one hand a red ball of mass
holds in one hand a red ball of mass ![]() that he throws at person
that he throws at person ![]() . We neglect gravity in this setup so that, if the merry-go-round were not spinning, the ball would fly in a straight line toward
. We neglect gravity in this setup so that, if the merry-go-round were not spinning, the ball would fly in a straight line toward ![]() (i.e. no projectile motion).
(i.e. no projectile motion).
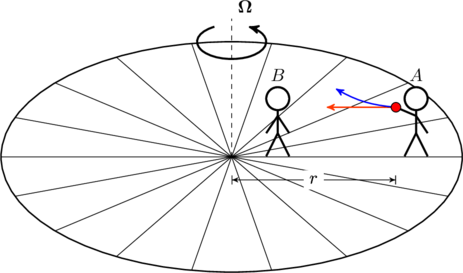
Let us try and understand how ![]() perceives the ball when the merry-go-round is spinning. He sees
perceives the ball when the merry-go-round is spinning. He sees ![]() throwing the ball straight at him, and expects the ball to travel straight towards him, as indicated by the orange line. However, at the instant the ball leaves
throwing the ball straight at him, and expects the ball to travel straight towards him, as indicated by the orange line. However, at the instant the ball leaves ![]() 's hand it has an angular momentum
's hand it has an angular momentum
(2) ![]()
This ![]() must be conserved as the ball travels toward
must be conserved as the ball travels toward ![]() . When the ball is at a radial distance
. When the ball is at a radial distance ![]() from the axis of rotation, we have
from the axis of rotation, we have
(3) ![]()
where ![]() is the angular velocity of the ball about the axis of the merry-go-round. Clearly,
is the angular velocity of the ball about the axis of the merry-go-round. Clearly,
(4) ![]()
which means the ball starts going around the axis faster than either ![]() or
or ![]() . Instead of coming straight at him,
. Instead of coming straight at him, ![]() will see the ball deflect in the direction of the spin under the influence of some invisible force (the blue line in the figure). This is nothing but the Coriolis force.
will see the ball deflect in the direction of the spin under the influence of some invisible force (the blue line in the figure). This is nothing but the Coriolis force.
Conversely, if ![]() were to throw the ball at
were to throw the ball at ![]() , then the angular velocity of the ball would decrease as it moves farther from the center, and
, then the angular velocity of the ball would decrease as it moves farther from the center, and ![]() would see the ball deflect in a direction opposite to the spin of the merry-go-round. In both cases, the ball is simply conserving angular momentum.
would see the ball deflect in a direction opposite to the spin of the merry-go-round. In both cases, the ball is simply conserving angular momentum.
We can be more precise. Let’s take a closer look at what happens immediately after the ball leaves ![]() 's hand in the figure above. In a short time
's hand in the figure above. In a short time ![]() the ball moves a small distance
the ball moves a small distance ![]() in the radial direction (
in the radial direction (![]() is negative here), and the angular velocity changes from
is negative here), and the angular velocity changes from ![]() to
to ![]() as a result. Then, by conservation of angular momentum
as a result. Then, by conservation of angular momentum
(5) ![]()
We can Taylor expand the terms in parantheses using ![]() ,
,
(6) ![]()
where the ![]() are higher order terms in
are higher order terms in ![]() and
and ![]() . Since these ratios are much smaller than
. Since these ratios are much smaller than ![]() the higher order terms are too small to cancel the first order terms, and the above equation is satisfied only if
the higher order terms are too small to cancel the first order terms, and the above equation is satisfied only if
(7) ![]()
From ![]() and
and ![]() 's perspective, the ball’s tangential velocity increases by
's perspective, the ball’s tangential velocity increases by ![]() in time
in time ![]() . The force responsible for this change is
. The force responsible for this change is
(8) ![]()
where in the second step we’ve used (7), and ![]() . Looking at (8), we see that it is exactly the expression from (1), once we work out the directions of the vectors.
. Looking at (8), we see that it is exactly the expression from (1), once we work out the directions of the vectors.
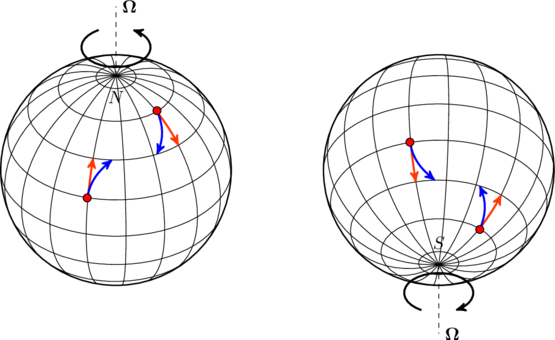
The advantage of thinking in terms of angular momentum conservation is that we can determine the direction the Coriolis force without having to deal with vectors. For instance, in the figure above, the mass ![]() is moving closer to the axis of Earth’s rotation, which means it must spin faster around the axis to conserve its angular momentum. This explains why the actual trajectory is the blue line. If
is moving closer to the axis of Earth’s rotation, which means it must spin faster around the axis to conserve its angular momentum. This explains why the actual trajectory is the blue line. If ![]() were moving away from the axis (toward the equator), it would deflect westward. The figure below shows these effects for both the northern and southern hemispheres.
were moving away from the axis (toward the equator), it would deflect westward. The figure below shows these effects for both the northern and southern hemispheres.
Applications
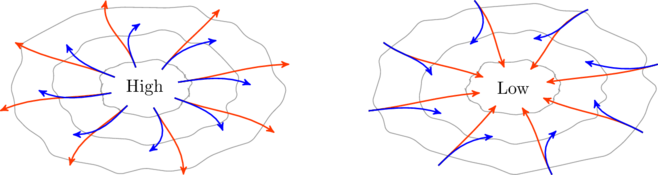
To see how the above insight may be helpful, let us consider a couple of qualitative examples. First, we look at cyclones in the northern hemisphere. Cyclones result from strong pressure gradients in the atmosphere, like the ones shown in the figure below (the gray lines are regions of constant pressure). For instance, if there is a high pressure region at the center of the cyclone air moves out. But the motion of air is modified by the Coriolis force in the manner described above; wind blowing toward the north is turned eastward and wind blowing south deflects toward the west, resulting in a clockwise circulation of air in the cyclone. The opposite happens if the cyclone has a low pressure center.
Another interesting application is the Focault pendulum, which demonstrates the rotation of Earth. It is just a pendulum where the bob moves over a large enough distance that the Coriolis effect is appreciable. For instance, as the pendulum swings north it deviates a little to the east (see figure). When it swings back it deviates to the west. The net result is a precession of the pendulum’s orbit, as shown in this animation (see chapter 9 of Kleppner and Kolenkow for a quantitative analysis).