JEE Advanced 2019 Paper 2, Question 6
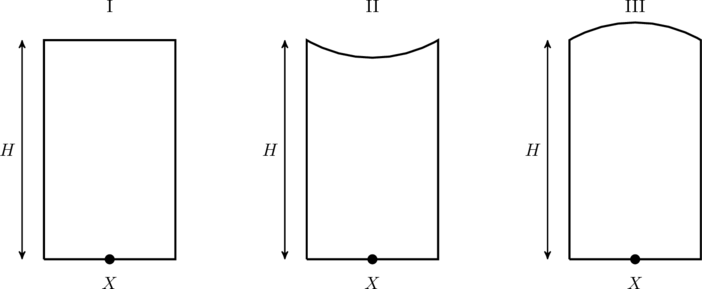
Three glass cylinders of equal height ![]() and same refractive index
and same refractive index ![]() are placed on a horizontal surface as shown in figure. Cylinder I has a flat top, cylinder II has a convex top and cylinder III has a concave top. The radii of curvature of the two curved tops are same (
are placed on a horizontal surface as shown in figure. Cylinder I has a flat top, cylinder II has a convex top and cylinder III has a concave top. The radii of curvature of the two curved tops are same (![]() ). If
). If ![]() , and
, and ![]() are the apparent depths of a point
are the apparent depths of a point ![]() on the bottom of the three cylinders, respectively, the correct statement(s) is/are:
on the bottom of the three cylinders, respectively, the correct statement(s) is/are:
Solution
We can get some intuition for what happens in each case by drawing some simple ray diagrams, as in the figure below. To simplify our analysis we can replace the convex and concave surfaces with a triangular surface as shown there; the argument remains the same for the actual spherical surfaces.
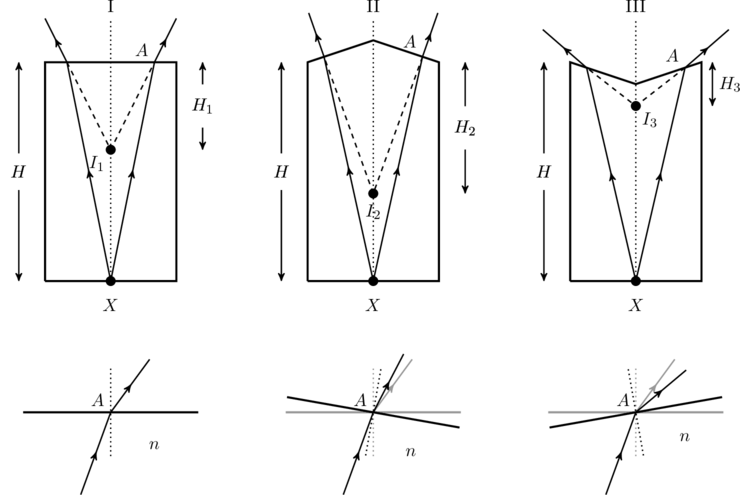
First, in cylinder I the observer would see a virtual image of the object ![]() at a new location
at a new location ![]() , obtained by extrapolating the refracted rays back into the medium. In the bottom row we have zoomed in on the point
, obtained by extrapolating the refracted rays back into the medium. In the bottom row we have zoomed in on the point ![]() at the cyclinder top to show how a ray refracts. Next, for cyclinder II a similar refraction happens, but the ray from medium
at the cyclinder top to show how a ray refracts. Next, for cyclinder II a similar refraction happens, but the ray from medium ![]() now makes a smaller angle of incidence with respect to the normal. As a result, it is deviates from its original direction to a lesser degree after refraction (see bottom row of the figure, the original refracted ray is shown in gray). Extending the refracted backwards we therefore find the image at
now makes a smaller angle of incidence with respect to the normal. As a result, it is deviates from its original direction to a lesser degree after refraction (see bottom row of the figure, the original refracted ray is shown in gray). Extending the refracted backwards we therefore find the image at ![]() which is closer to the original point
which is closer to the original point ![]() . Finally, for cylinder III the opposite happens — the rays from medium
. Finally, for cylinder III the opposite happens — the rays from medium ![]() are incident at a larger angle than in the flat case, which means they are refracted by a larger angle. Extending it backward, we find the image at
are incident at a larger angle than in the flat case, which means they are refracted by a larger angle. Extending it backward, we find the image at ![]() which is shallower than
which is shallower than ![]() . We can thus conclude that
. We can thus conclude that
(1) ![]()
which means option (B) is incorrect, but options (A) and (C) are correct.
More prosaically, we can solve this problem by using the following relation between object and image distances for a refracting surface of radius ![]() (see figure),
(see figure),
(2) ![]()
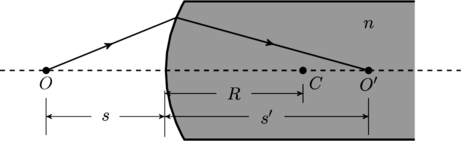
A derivation of this formula is given in chapter 27 of the Feynman lectures vol. I. The signs of ![]() and
and ![]() are positive in the figure. Note that the formula also applies if the direction of the rays are reversed. We keep the object
are positive in the figure. Note that the formula also applies if the direction of the rays are reversed. We keep the object ![]() at
at ![]() which means
which means ![]() . For the flat surface in case I we can take
. For the flat surface in case I we can take ![]() in (2), to find
in (2), to find
(3) ![]()
The negative value of ![]() means the point
means the point ![]() is inside the refracting medium
is inside the refracting medium ![]() , as expected. Thus,
, as expected. Thus, ![]() . For cylinder II, the radius of curvature is
. For cylinder II, the radius of curvature is ![]() , and (2) gives
, and (2) gives
(4) ![]()
Therefore ![]() , which means
, which means ![]() just as we inferred above. Finally, cylinder III has a radius of curvature is
just as we inferred above. Finally, cylinder III has a radius of curvature is ![]() , which makes (2)
, which makes (2)
(5) ![]()
and therefore ![]() is smaller than
is smaller than ![]() . Thus, we recover (1). It is also clear that
. Thus, we recover (1). It is also clear that
(6) ![]()
which is less than ![]() . So option (D) is incorrect.
. So option (D) is incorrect.
Tip: The qualitative analysis at the beginning is to help with your conceptual understanding. In the actual exam it is always safer to rely on the formula rather than crude hand drawn ray diagrams.