Oblique beam on a double slit

JEE Advanced 2019 Paper 2, Question 7

In a Young’s double slit experiment, the slit separation $d$ is 0.3 mm and the screen distance $D$ is 1 m. A parallel beam of light of wavelength 600 nm is incident on the slits at angle $\alpha$ as shown in figure. On the screen, the point $O$ is equidistant from the slits and distance $P O$ is 11.0 mm. Which of the following statement(s) is/are correct?

Rendered by QuickLaTeX.com

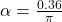For $\alpha=\frac{0.36}{\pi}$ degree, there will be destructive interference at point $O$ .
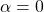For $\alpha=0$ , there will be constructive interference at point $P$ .
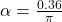For $\alpha=\frac{0.36}{\pi}$ degree, there will be destructive interference at point $P$ .
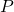Fringe spacing depends on $\alpha$ .

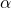Solution

This setup is different from the usual double slit experiment in that there is an extra phase shift introduced by the angle of the incident beam, $\alpha$ . This introduces an extra path difference of $d \sin \alpha$ between the two rays. Of course, there is also the path difference $yd/D$ incurred after light passes through the slits. Therefore the two light wavees arrive at the screen with a total path difference of

(1) $\begin{equation*} \Delta = d \sin \alpha + \frac{y d}{D} \end{equation*}$

Rendered by QuickLaTeX.com

If we express $\alpha$ in radians, we can approximate $d \sin \alpha \approx d \alpha$ for small values of $\alpha$ . Again, note that it is crucial we represent $\alpha$ in radians when we do this. Furthermore, we have constructive interference when the path difference is an integer multiple of full wavelengths, and it is destructive when it is a half-integer multiple. That is,

(2) $\begin{equation*} \Delta \approx d \alpha + \frac{y d}{D} = \begin{cases} m \lambda, &\text{ (constructive)} \\ (m+\frac{1}{2})\lambda, &\text{ (destructive)} . \end{cases} \end{equation*}$

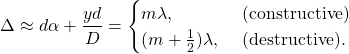
We can now consider each option given in the problem. First we note that $\alpha = \frac{0.36}{\pi}$ degrees is

(3) $\begin{equation*} \alpha = \frac{0.36}{\pi} \times \frac{\pi}{180} = 2 \times 10^{-3} \text{ radians} . \end{equation*}$

At point $O$ on the screen $y=0$ , and by (2)

(4) $\begin{equation*} \Delta = 0.3 \text{ mm} \times 2 \times 10^{-3} \text{ rad} = 600 \text{ nm}, \end{equation*}$

which is exactly one wavelength ( $m=1$ ), ensuring constructive interference at $O$ . So option (A) is incorrect.

For $\alpha=\frac{0.36}{\pi}$ degrees, at point $P$ ( $y=11 \text{ mm}$ ),

(5) $\begin{equation*} \Delta = 0.3 \text{ mm} \times 2 \times 10^{-3} \text{ rad } + \frac{11 \text{ mm} \times 0.3 \text{ mm}}{1 \text{ m}} = 3900 \text{ nm } \equiv 6.5 \lambda \end{equation*}$

which means we have destructive interference at $P$ . If $\alpha$ were zero, we’d have $\Delta = 3300 \equiv 5.5 \lambda$ , which would also mean destructive interference. So option (B) is incorrect, but option (C) is correct.

Finally, we note that the additional path difference $d \alpha$ shifts all the fringes uniformly; the spacing between the fringes is still

(6) $\begin{equation*} y_{m+1}-y_m = \frac{d}{D} , \end{equation*}$

which is independent of $\alpha$ . Therefore, option (D) is incorrect.

Leave a Reply Cancel reply