JEE Advanced 2018 Paper 1, Question 1
The potential energy of a particle of mass ![]() at a distance
at a distance ![]() from a fixed point
from a fixed point ![]() is given by
is given by ![]() , where
, where ![]() is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius
is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius ![]() about the point
about the point ![]() . If
. If ![]() is the speed of the particle and
is the speed of the particle and ![]() is the magnitude of its angular momentum about
is the magnitude of its angular momentum about ![]() , which of the following statements is (are) true?
, which of the following statements is (are) true?
Solution
The force due to the given potential is
(1) ![]()
The mass also experiences a centrifugal force due to its circular motion,
(2) ![]()
For the orbit to remain circular the net radial force on the mass must be zero at ![]() . That is,
. That is,
(3) 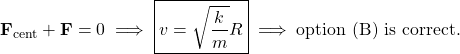
The angular momentum ![]() for a circular orbit takes on the simple form
for a circular orbit takes on the simple form ![]() since
since ![]() and
and ![]() are perpendicular to one another. Substituting the speed calculated above,
are perpendicular to one another. Substituting the speed calculated above,
(4) ![]()
Advanced tidbit: There is a theorem in classical mechanics, called Bertrand’s theorem, which states that the only central potentials for which all bound orbits are closed are the simple harmonic potential ![]() and the graviational/electrostatic potential
and the graviational/electrostatic potential ![]() .
.
That means, for instance a potential ![]() will not, in general, produce a bound orbit that closes in on itself. However, circular orbits are a special case; we can indeed have a circular orbits for
will not, in general, produce a bound orbit that closes in on itself. However, circular orbits are a special case; we can indeed have a circular orbits for ![]() if the centrifugal force cancels the force due to the potential exactly. But if we disturb the circular orbit slightly, the new path will not come back to the same point in space after one period of revolution.
if the centrifugal force cancels the force due to the potential exactly. But if we disturb the circular orbit slightly, the new path will not come back to the same point in space after one period of revolution.