Resistor network with mirror symmetry

JEE Advanced 2012 Paper 1, Question 12

For the resistance network shown in the figure, choose the correct option(s).

Rendered by QuickLaTeX.com

The current through 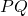$PQ$ is zero.
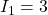$I_1 = 3$ A.
The potential at 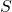$S$ is less than that at $Q$ .
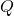$I_2 = 2$ A.

Solution

We can speed up the solution by noticing the mirror symmetry of the circuit. Let the current $I_1$ split into two parts $I_a$ and $I_b$ at the node $X$ (see figure). Similarly, let the currents going into node $Y$ be $I_a'$ and $I_b'$ . If we were to reverse the polarity of the $12 \, {\rm V}$ battery connected to the circuit, all currents would simply reverse direction, but their magnitudes would remain the same. But then, the currents leaving the node $Y$ must be $I_a$ and $I_b$ since, from the battery’s perspective, the circuit looks the same under $X \leftrightarrow Y$ . Thus, $I_a'=I_a$ and $I_b'=I_b$ .

By similar reasoning the currents through the 1 $\Omega$ resistors must be the same, and we label these $I_\Delta$ . Using Kirchoff’s current law we can fill in the remaining currents through $PS$ and $QT$ (see figure below).

Applying Kirchoff’s voltage law on the loop $XPQ$ ,

Similarly, the loop $PQTS$ gives

(1) $\begin{equation*} -2 (I_a + I_\Delta) - I_\Delta + 4 (I_b - I_\Delta) - I_\Delta = 0 \end{equation*}$

Clearly, both of these equations can only be satisfied if $I_\Delta = 0$ . So option (A) is correct.

Since no current flows through the 1 $\Omega$ resistors and we can treat the legs $XPSY$ and $XQTY$ as independent. Then,

(2) $\begin{equation*} I_2 = I_a = \frac{12 \, \rm{V}}{6 \, \Omega} = 2 \, {\rm A} \implies \text{ \bf option (D) is correct} , \end{equation*}$

and the total current $I_1$ is

(3) $\begin{equation*} I_1 = I_a + I_b = \frac{12 \, \rm{V}}{6 \, \Omega} + \frac{12 \, \rm{V}}{12 \, \Omega} = 3 \, {\rm A} \implies \text{ \bf option (B) is correct} , \end{equation*}$

The potential at point $S$ is $V_S = 2 I_a = 4 \, {\rm V}$ , and that at point $Q$ is $V_Q = 8 I_b = 8 \, {\rm V}$ , and so $V_S < V_Q$ which means option (C) is correct.

This, all the given options are correct.

Leave a Reply Cancel reply