JEE Advanced 2019 Paper 2, Question 4
An electric dipole with dipole moment ![]() is held fixed at the origin
is held fixed at the origin ![]() in the presence of an uniform electric field of magnitude
in the presence of an uniform electric field of magnitude ![]() . If the potential is constant on a circle of radius
. If the potential is constant on a circle of radius ![]() centered at the origin as shown in figure, then the correct statement(s) is/are:
centered at the origin as shown in figure, then the correct statement(s) is/are:
(![]() is permittivity of free space.
is permittivity of free space. ![]() dipole size)
dipole size)
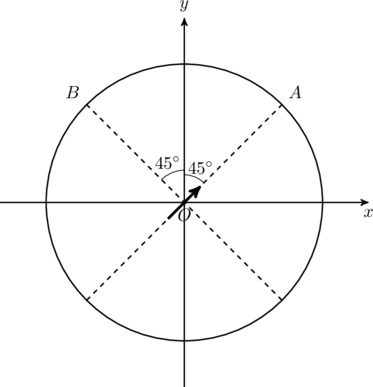
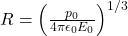
- Total electric field at point
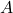 is
is 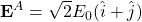
- Total electric field at point
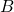 is
is 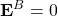
- The magnitude of total electric field on any two points of the circle will be same.
Solution
The potential due to the dipole kept at the origin is
(1) ![]()
We’re also told that there is a uniform electric field of magnitude ![]() present, but we don’t know its direction. The combination of this electric field with that due to the dipole creates an equipotential surface, which is the circle of radius
present, but we don’t know its direction. The combination of this electric field with that due to the dipole creates an equipotential surface, which is the circle of radius ![]() . Let us take
. Let us take ![]() to point along the unit vector
to point along the unit vector ![]() where
where ![]() . That is,
. That is,
(2) ![]()
If we denote the potential associated with this field as ![]() , then
, then ![]() , which means
, which means
(3) ![]()
where ![]() is a constant. We’re unconcerned with what happens in the
is a constant. We’re unconcerned with what happens in the ![]() direction, so we ignore the potential along
direction, so we ignore the potential along ![]() . A point on the circle of radius
. A point on the circle of radius ![]() is given
is given
(4) ![]()
where ![]() is the angle with respect to the positive
is the angle with respect to the positive ![]() -axis. By superposition, the total potential at this point is
-axis. By superposition, the total potential at this point is
(5) ![]()
where we have used ![]() . This potential will be a constant if we choose
. This potential will be a constant if we choose
(6) ![]()
That means ![]() , and
, and ![]() . Therefore
. Therefore
(7) ![]()
Substituting ![]() in (2) we also find that
in (2) we also find that
(8) ![]()
To find the electric fields at points ![]() and
and ![]() we need to add the field due to the dipole to
we need to add the field due to the dipole to ![]() . This is
. This is
(9) 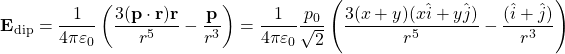
The point ![]() has the co-ordinates
has the co-ordinates ![]() . Therefore, the field at this point is
. Therefore, the field at this point is
(10) ![]()
Similarly, the dipole field at ![]() is
is
(11) ![]()
Adding the uniform field from (8), we find that the total electric field at these points are
(12) ![Rendered by QuickLaTeX.com \begin{align*} {\bf E}^A = \left( \sqrt{2} + \frac{1}{\sqrt{2}} \right) E_0 (\hat{i}+\hat{j}) &\implies \text{ option (B) is incorrect. } \\[1em] {\bf E}^B = 0 &\implies \text{ option (C) is correct. } \end{align*}](https://www.jeefirst.com/wp-content/ql-cache/quicklatex.com-f9d5142a5694c7296ea0d31ce3056d1d_l3.png)
Just from examining the points ![]() and
and ![]() we also see that the magnitude of the electric field cannot be the same at all point of the circle. That means, option (D) is incorrect as well.
we also see that the magnitude of the electric field cannot be the same at all point of the circle. That means, option (D) is incorrect as well.
Commentary: This problem seems particularly lengthy for the JEE exam. If there is a simpler way to do this problem, please let me know. It is certainly possible to notice some symmetries of the setup to calculate ![]() without using the formula in (9), but I doubt if it will save much time.
without using the formula in (9), but I doubt if it will save much time.