JEE Advanced 2019 Paper 2, Question 12
A perfectly reflecting mirror of mass ![]() mounted on a spring constitutes a spring-mass system of angular frequency
mounted on a spring constitutes a spring-mass system of angular frequency ![]() such that
such that ![]() with
with ![]() as Planck’s constant.
as Planck’s constant. ![]() photons of wavelength
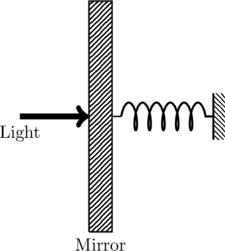
photons of wavelength ![]() strike the mirror simultaneously at normal incidence such that the mirror gets displaced by
strike the mirror simultaneously at normal incidence such that the mirror gets displaced by ![]() .
.
If the value of ![]() is
is ![]() , what is the value of
, what is the value of ![]() ?
?
[Consider the spring as massless]
Solution
The momentum carried by a single photon is given by the de Broglie relation ![]() . The total momentum carried by
. The total momentum carried by ![]() photons is therefore
photons is therefore ![]() . All the photons hit the mirror simultaneously and are reflected back perfectly by the mirror. So the total momentum of the photons after collision is
. All the photons hit the mirror simultaneously and are reflected back perfectly by the mirror. So the total momentum of the photons after collision is ![]() , with the minus indicating the change in direction of the photons. By conservation of momentum,
, with the minus indicating the change in direction of the photons. By conservation of momentum,
(1) ![]()
That is, the photons impart a momentum ![]() to the mirror. The mirror will move forward and will come to a stop when all of its kinetic energy has been converted to potential energy stored in the spring. That is,
to the mirror. The mirror will move forward and will come to a stop when all of its kinetic energy has been converted to potential energy stored in the spring. That is,
(2) ![]()
where ![]() is the distance by which the spring compresses. Substituting (1) and inverting, we obtain
is the distance by which the spring compresses. Substituting (1) and inverting, we obtain
(3) ![]()
In the last step we’ve used the fact that ![]() for a mass-spring system to write
for a mass-spring system to write ![]() .
.
We can now use the relation ![]() given in the problem, and plug in
given in the problem, and plug in ![]() and
and ![]() to find
to find
(4) ![]()
From this we read off ![]() .
.
Tip: Notice how using conservation of energy helped us relate ![]() to the displacement
to the displacement ![]() directly in (2). Had we analyzed this problem in terms of the forces due to the photons and the spring, it would take some more steps to find this relation. As a general rule, whenever you have a situation where the initial and final energies are purely kinetic energy or purely potential energy, it is easier to use conservation of energy.
directly in (2). Had we analyzed this problem in terms of the forces due to the photons and the spring, it would take some more steps to find this relation. As a general rule, whenever you have a situation where the initial and final energies are purely kinetic energy or purely potential energy, it is easier to use conservation of energy.