JEE Advanced 2019 Paper 2, Question 2
A block of mass ![]() is attached to a massless spring with spring-constant
is attached to a massless spring with spring-constant ![]() . This block is connected to two other blocks of masses
. This block is connected to two other blocks of masses ![]() and
and ![]() using two massless pulleys and strings. The accelerations of the blocks are
using two massless pulleys and strings. The accelerations of the blocks are ![]() and
and ![]() as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is
as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is ![]() . Which of the following option(s) is/are correct?
. Which of the following option(s) is/are correct?
[![]() is the acceleration due to gravity. Neglect friction]
is the acceleration due to gravity. Neglect friction]

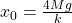
- When spring achieves an extension of
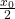 for the first time, the speed of the block connected to the spring is
for the first time, the speed of the block connected to the spring is 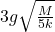
- At an extension of
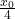 of the spring, the magnitude of acceleration of the block connected to the spring is
of the spring, the magnitude of acceleration of the block connected to the spring is 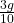
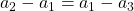
Solution
WARNING: I am unsure whether I’ve made some mistake in my solutions, so please try this problem yourself and let me know if you get a different answer.

From the force diagram, we have
(1) 
To relate the accelerations we use the constraint that the lengths of the strings connecting the masses are constant. Then,
(2) ![]()
where ![]() is the radius of the second pulley and
is the radius of the second pulley and ![]() is the length of the string around it. Differentiating this expression twice w.r.t. we get
is the length of the string around it. Differentiating this expression twice w.r.t. we get
(3) ![]()
We’ve also marked the initial position of the block attached to the spring by ![]() with its displacement
with its displacement ![]() at some later time. Then,
at some later time. Then,
(4) ![]()
Next, we note that ![]() and
and ![]() for the directions indicated. Thus, from (3) and (4),
for the directions indicated. Thus, from (3) and (4),
(5) ![]()
Using the above relation we can eliminate ![]() from the equations (1),
from the equations (1),
(6) 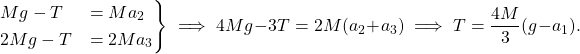
Keeping in mind that ![]() , we obtain
, we obtain
(7) ![]()
This equation represents simple harmonic motion about the equilibrium point ![]() , where the acceleration
, where the acceleration ![]() . Since the oscillations were started at
. Since the oscillations were started at ![]() with zero initial velocity, the solution to the differential equation (7) is
with zero initial velocity, the solution to the differential equation (7) is
(8) ![]()
with ![]() . This is the blue line in the figure below. The maximum extension
. This is the blue line in the figure below. The maximum extension ![]() is corresponds to
is corresponds to ![]() ,
,
(9) ![]()
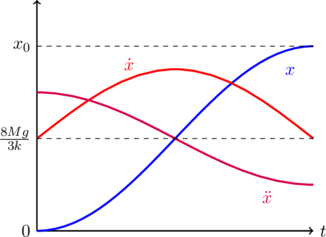
The point ![]() is just the equilibrium point, where the velocity reaches its maximum possible value
is just the equilibrium point, where the velocity reaches its maximum possible value ![]() , which is
, which is
(10) 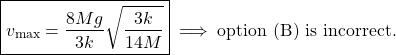
Finally, the acceleration at ![]() can be calculated directly from (7) by setting
can be calculated directly from (7) by setting ![]() ,
,
(11) ![]()