JEE Advanced 2019 Paper 2, Question 1
A thin and uniform rod of mass ![]() and length
and length ![]() is held vertical on a floor with large friction. The rod is released from rest so that it falls by rotating about its contact-point with the floor without slipping. Which of the following statement(s) is/are correct, when the rod makes an angle
is held vertical on a floor with large friction. The rod is released from rest so that it falls by rotating about its contact-point with the floor without slipping. Which of the following statement(s) is/are correct, when the rod makes an angle ![]() with vertical?
with vertical?
[![]() is the acceleration due to gravity]
is the acceleration due to gravity]
- The angular speed of the rod will be
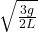
- The angular acceleration of the rod will be
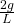
- The radial acceleration of the rod’s center of mass will be
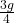
- The normal reaction force from the floor on the rod will be
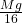
Solution
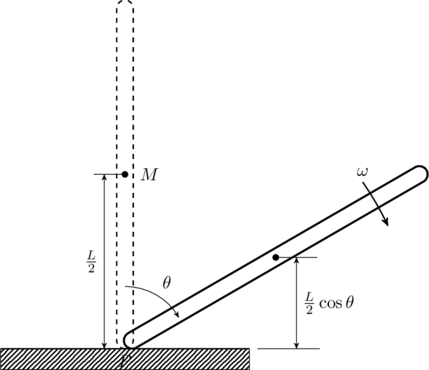
The quickest way to find the angular speed ![]() is to use conservation of energy. Initially, all of the energy in the system is stored as potential energy. For an extenstive object like the rod we can find the potential energy by locating the center of mass (C.o.M) of the rod, which is at a height
is to use conservation of energy. Initially, all of the energy in the system is stored as potential energy. For an extenstive object like the rod we can find the potential energy by locating the center of mass (C.o.M) of the rod, which is at a height ![]() above ground level. Therefore, the initial energy is
above ground level. Therefore, the initial energy is
(1) ![]()
When the rod has fallen by an angle ![]() with respect to the vertical, the total energy will be the sum of potential energy of the C.o.M at height
with respect to the vertical, the total energy will be the sum of potential energy of the C.o.M at height ![]() , and the kinetic energy of the falling rod,
, and the kinetic energy of the falling rod,
(2) ![]()
where ![]() is the moment of inertia of the rod about the pivot
is the moment of inertia of the rod about the pivot ![]() . Since energy is conserved
. Since energy is conserved
(3) ![]()
Plugging in ![]() and
and ![]() , we find
, we find
(4) 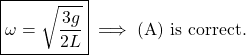
To find the angular acceleration ![]() , we can just differentiate (3) w.r.t. time,
, we can just differentiate (3) w.r.t. time,
(5) 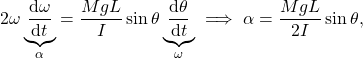
which simplifies to
(6) 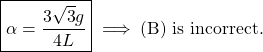
Another way to find the angular acceleration is to equate the two expressions for torque ![]() and
and ![]() (see figure),
(see figure),
(7) ![]()
which gives the same expression as (5).
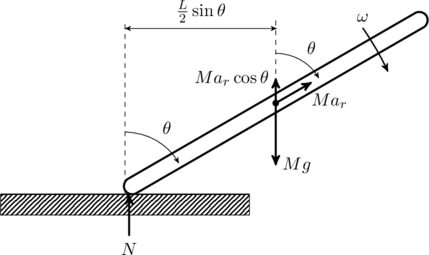
The radial acceleration of the C.o.M is
(8) 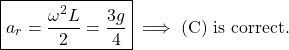
Finally, the normal reaction from the floor ![]() supports the weight of the rod, minus the vertical component of the radial force,
supports the weight of the rod, minus the vertical component of the radial force,
(9) ![]()
which works out to
(10) ![]()