An infinite ladder of resistors

Problem 3.152 of Irodov

The figure below shows an inifite circuit formed by the repetition of the same link, consisting of resistance $R_1 = 4.0 \ \Omega$ and $R_2 = 3.0 \ \Omega$ . Find the resistance of this circuit between points $A$ and $B$ .

Rendered by QuickLaTeX.com

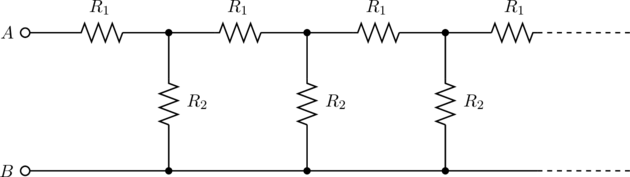
Solution

Let’s denote the resistance between the points $A$ and $B$ by $R_{AB}$ . Since the circuit is infinite, removing the first $R_1$ and $R_2$ resistors gives the same arrangement back again — the arrangement is self-similar. That means, the resistance between the points $C$ and $D$ is just $R_{AB}$ without the left-most $R_1$ and $R_2$ resistors, and we may redraw the circuit as shown below.

Rendered by QuickLaTeX.com

It is now straightforward to calculate the resistance,

(1) $\begin{equation*} R_{AB} = R_1 + \frac{R_2 R_{AB}}{R_2 + R_{AB}} \end{equation*}$

which gives a quadratic equation for $R_{AB}$ ,

(2) $\begin{equation*} R_{AB}^2 - R_1 R_{AB} - R_1 R_2 = 0 . \end{equation*}$

This equation has two roots. We keep only the positive root, because resistance cannot be a negative number.

(3) $\begin{equation*} \boxed{ R_{AB} % = \frac{R_1 \pm \sqrt{R_1^2 + 4 R_1 R_2}}{2} = \frac{R_1}{2} \left( 1 + \sqrt{ 1 + \frac{4 R_2}{R_1} } \right) } . \end{equation*}$

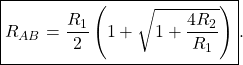
Plugging in $R_1 = 4.0 \ \Omega$ and $R_2 = 3.0 \ \Omega$ , we find $R_{AB} = 6.0 \ \Omega$ .

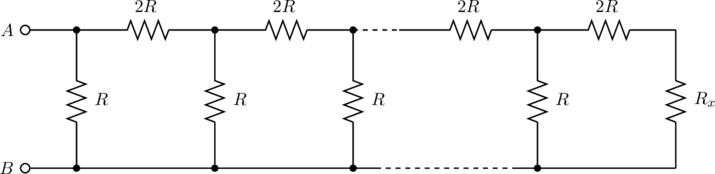
Bonus Problem: At what value of the resistance $R_x$ in the circuit shown below will the total resistance between points $A$ and $B$ be independent of the number of cells. (Hint: What value of $R_x$ will make the circuit appear self-similar at the lower rungs of the ladder?)

Rendered by QuickLaTeX.com

Answer: $(\sqrt{3}-1)R$ .

Leave a Reply Cancel reply